J'ai essayé de suggérer une explication à ce que pouvait être le machine learning. Je vous propose maintenant d'étudier un cas concret avec une implémentation en javascript. Avertissement : ce billet utilise intensément javascript et svg, si vous le consultez sur un lecteur rss, je vous conseille de passer à la version Web.

Entendons-nous bien, javascript n'est probablement pas le langage le plus adapté à ce type d'usage. Nous l'utiliserons uniquement pour que vous puissiez faire tourner le prototype directement dans votre navigateur.

Grâce au machine learning, on peut réaliser des applications extraordinaires, comme de la reconnaissance faciale de patron relou. Néanmoins, pour aborder les concepts utiles en douceur, nous allons voir une application beaucoup plus simple.

Liste des courses

Rappelons les grossières étapes à suivre dans la mise en place d'un projet de machine learning :

1. formaliser un problème ;
2. imaginer un modèle (une fonction) adapté à la résolution du problème ;
3. déterminer les caractéristiques pertinentes à passer à notre modèle ;
4. recueillir et préparer les données d'apprentissage ;
5. déterminer les paramètres de notre modèle grâce à un algorithme d'apprentissage ;
6. profiter.

Nous parlons ici de la mise en place d'un prototype rapide et cradingue. Dans un contexte de production, on réfléchira aussi à la sélection de métriques de pertinence, on itérera pour trouver le modèle le plus adéquat possible, on pré-traitera nos données pour éliminer d'éventuelles aberrations statistiques et optimiser la phase d'apprentissage, etc. Par ailleurs, j'essaye de vulgariser un peu ; pour aller plus loin, il existe des ressources très bien faites.

Formaliser le problème, ou « Martine cherche un logement »

Martine vient d'arriver dans la région et cherche un logement. En consultant les annonces immobilières sur le Bon Coin, elle trouve des studio délabrés dans le centre ville de Montpellier pour un loyer de 850€, et se demande si ce tarif exorbitant est représentatif du marché local, ou le fruit d'un·e propriétaire ayant légèrement abusé du crack.

Martine n'étant pas dépourvue de talent, elle décide d'utiliser les technologies de pointe pour se faire une meilleure idée du coût moyen d'un logement. La question qu'elle se pose est la suivante : étant donnée la surface d'un logement dans l'agglomération montpelliéraine, quel sera le montant moyen du loyer mensuel ?

Déterminer le modèle adapté au problème

Le modèle, c'est la fonction dans laquelle on va fourrer nos données (la surface) et qui va cracher notre réponse (le montant du loyer).

Déterminer le bon modèle, c'est imaginer quelle pourrait être la tête de notre fonction. Est-ce une droite ? Une courbe ? Un zigouigoui qui monte et qui descend (notez à quel point j'évite d'employer un vocabulaire mathématique dans un héroïque soucis de vulgarisation) ?

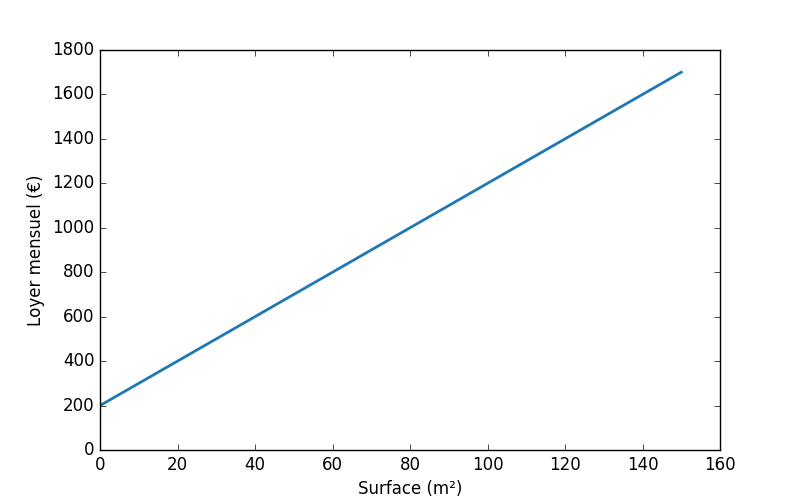
Je vais émettre une hypothèse un peu simpliste (mais rien ne nous empêchera d'itérer ensuite) : il existe une relation linéaire entre la surface d'un logement et le montant du loyer. C'est à dire que si je dessine la relation entre la surface et loyer, je vais obtenir grosso-modo un truc un peu comme ça :

Ce type de droite peut mathématiquement être exprimé à travers ce type de relation :

$$f(x) = a * x + b$$

Ou a et b sont des nombres réels.

Ici, a et b sont les paramètres de notre modèle : ce sont ces nombres que l'on souhaite déterminer. Les fort·e·s en maths auront reconnu qu'il s'agit d'un problème de régression linéaire, les autres peuvent se contenter d'ignorer paisiblement ces termes vulgaires.

Pour être honnête, il n'y a pas besoin de machine learning pour déterminer un modèle à deux paramètres, mais comme il n'y a pas de différence fondamentale avec un modèle avec 10 millions de paramètres au niveau du processus, autant utiliser l'exemple le plus simple possible.

Je vais ici apporter quelques ajustements au niveau de la nomenclature. Pour respecter la notation consacrée, je vais renommer ma fonction f en h (pour hypothèse, autre nom qu'on donne au modèle). Et au lieu des paramètres a et b, je vais utiliser le symbole θ (prononcer « theta »), histoire d'avoir une notation qui fonctionne pour un nombre variable de pramètres.

Ma fonction s'écrira donc :

$$h_\theta(x) = \theta_0 + \theta_1 * x$$

Déterminer les caractéristiques à passer au modèle

Les caractéristiques (en anglais : features) sont les données à fournir au modèle, c'est à dire les paramètres à passer à la fonction h.

Notre fonction h simpliste prends un seul paramètre : la surface du logement. Néanmoins, on pourrait imaginer une fonction à plusieurs paramètres : surface, numéro de l'étage, présence d'un balcon ou non, etc.

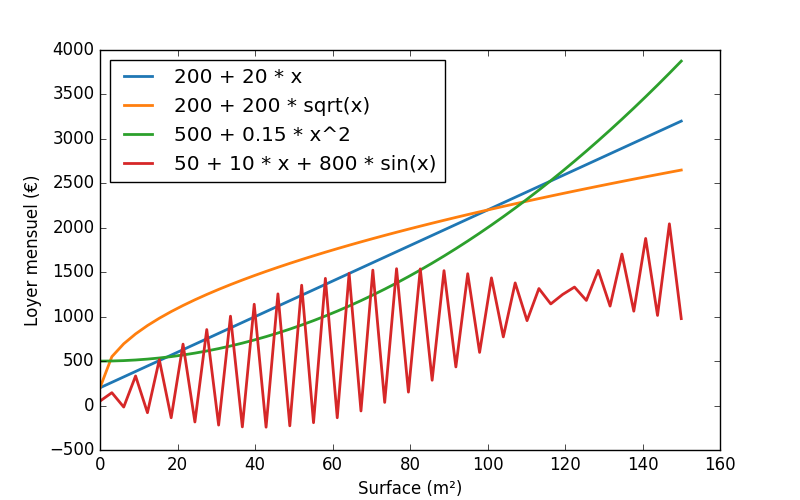
Par ailleurs, il est tout à fait possible de combiner des caractéristiques entre elles pour en fabriquer de nouvelles. Si je suspecte le montant du loyer d'évoluer, non pas en relation avec la surface, mais avec le carré de la surface, ou la racine de la surface, j'ai tout à fait le droit de créer le modèle suivant :

$$h_\theta(x) = \theta_0 + \theta_1 * x + \theta_2 * x^2 + \theta_3 * \sqrt{x}$$

Évidemment, si les caractéristiques évoluent, alors le modèle risque d'évoluer aussi, et inversement. Ces deux étapes sont donc à effectuer en parallèle.

Recueillir et préparer les données d'apprentissage

Pour entraîner notre modèle, il nous faut des données. Sachez que j'ai utilisé de véritables données, compilées par les Observatoire locaux des loyers et hébergées sur la plateforme open-data du gouvernement.

J'ai nettoyé le fichier csv pour ne conserver que les colonnes qui m'intéressent et les lignes concernant la région de Montpellier. Le résultat contient 300 lignes (suffisant pour entraîner un modèle à deux paramètres) et ressemble à ceci :

surface,loyer_mensuel
25,370
25,370
26,430
26,424
…
99,935
99,860
100,976
100,913

Le fichier est disponible.

On note traditionnellement « m » la quantité de données d'apprentissage.

Par ailleurs, pour l'entrée n° i dans la liste des données, on note x_i la surface, et y_i la réponse attendue, c'est-à-dire le loyer mensuel. Exemple : x₁ = 25, y₁ = 370.

Notez que pour faciliter le travail de l'algorithme de l'apprentissage, il est utile que les données soient du même ordre de grandeur. Nous pourrions donc pré-traiter les données pour que chaque valeur se retrouve dans l'intervalle [0; 1], par exemple. On parle de feature scaling. Pour rester le plus simple possible, nous sauterons cette étape.

Entraîner le modèle

Hop ! hop ! hop ! 150 pompes ! et que ça saute, limaçon !

Nous avons déterminé que notre modèle était une fonction linéaire à deux paramètres. Ces paramètres ne sont pas encore déterminés, c'est là le rôle de la phase d'apprentissage.

Le concept de l'algorithme d'apprentissage est relativement intuitif, mais comprendre la formule exacte qui permet de l'implémenter nécessite de se replonger dans le calcul différentiel, ce qui me semble hors sujet dans un billet de vulgarisation. Je vais tâcher d'expliquer le fonctionnement dans les grandes lignes, mais sans rentrer dans les détails techniques.

Nous cherchons donc à déterminer les valeurs de θ₀ et θ₁ telles que notre hypothèse produise des résultats les plus proches possibles des données à notre disposition. En d'autres termes, on veut qu'il y ait le moins d'écart possible entre h_θ(x_i) et y_i pour toutes les valeurs de i de 1 à m.

Fonction de coût

Pour mesurer cet écart, nous allons faire appel à une fonction que nous noterons J et qui prendra en paramètre un modèle donné (c'est à dire une valeur fixée pour θ₀ et θ₁). Cette fonction va calculer la moyenne des écarts entre h_θ(x_i) et y_i pour l'ensemble de nos données d'apprentissage.

J est nommée fonction de coût (cost function).

Concrètement, si J(θ₀, θ₁) est tout petit, glop ! glop ! les prédictions de notre modèle sont conformes à la réalité. Si J(θ₀, θ₁) est très grand, pas glop ! les prédictions de notre modèle sont à côté de la plaque.

Je vous donne la définition formelle de J, mais vous n'êtes pas obligé de vraiment vous y intéresser du moment que vous comprenez le principe.

$$J(\theta_0, \theta_1) = \frac{1}{2m} ((h_\theta(x_1) - y_1)^2 + (h_\theta(x_2) - y_2)^2 + \ldots + (h_\theta(x_m) - y_m)^2)$$

Ce qui peut aussi s'écrire sous cette forme, parfaitement équivalente (rappel : ∑ est le symbole qui signifie « somme ») :

$$J(\theta_0, \theta_1) = \frac{1}{2m}\sum_{i=1}^{m} (h_\theta(x_i) - y_i)^2$$

Précision 1 : on met (h_θ(x_i) - y_i) au carré pour que la valeur soit toujours positive.

Précision 2 : vous aurez peut-être remarqué que dans le calcul de la moyenne, on divise par 2m et pas par m. C'est parce que ça ne change rien tout en simplifiant d'obscurs calculs un peu plus loin. Ne vous en occupez pas.

Algorithme du gradient

Pour trouver les meilleures valeurs possibles pour θ₀ et θ₁, il suffit de trouver la valeur minimale de J.

Relisez la phrase précédente jusqu'à ce que vous soyez entièrement et absolument convaincu·e de sa véracité, car c'est la plus importante de tout le billet. Si vous comprenez cette phrase, vous comprenez le machine learning. N'est-ce pas limpide ? Si j'ai une fonction qui calcule à quel point mon modèle est à côté de la plaque, dés que je trouve sa valeur minimale, c'est que j'ai découvert le meilleur modèle possible, non ?

Nous sommes d'accord sur le principe, comment s'y prendre en pratique ?

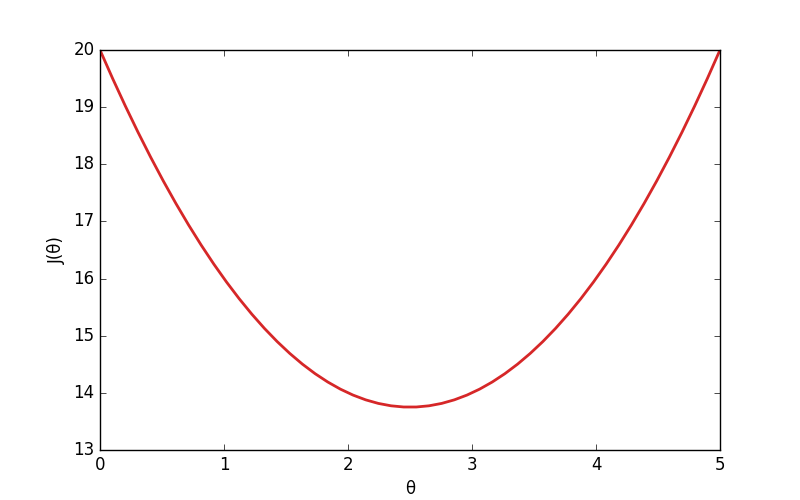
Commençons par représenter visuellement J pour clarifier les choses. Je vais encore simplifier en prétendant que mon modèle utilise un seul paramètre θ, et que donc J prends un seul paramètre.

À quoi ressemble J(θ) ? D'abord, J(θ) atteint un minimum lorsque je m'approche de la valeur optimale de θ. Plus je m'éloigne de cette valeur, plus J(θ) augmente. La fonction a donc une tronche qui devrait peu ou prou ressembler à ça :

Sur cet exemple, je pourrais déterminer la bonne valeur de θ à l'œil nu, mais ça devient impossible si le modèle contient plus de quelques paramètres (et à fortiori des millions).

Lorsque j' initialise mon modèle, je donne à θ une valeur aléatoire. Imaginons que θ = v₀, avec v₀ n'importe quel nombre (ici, 0.5). Je calcule le coût initial C₀ de mon modèle : J(v₀).

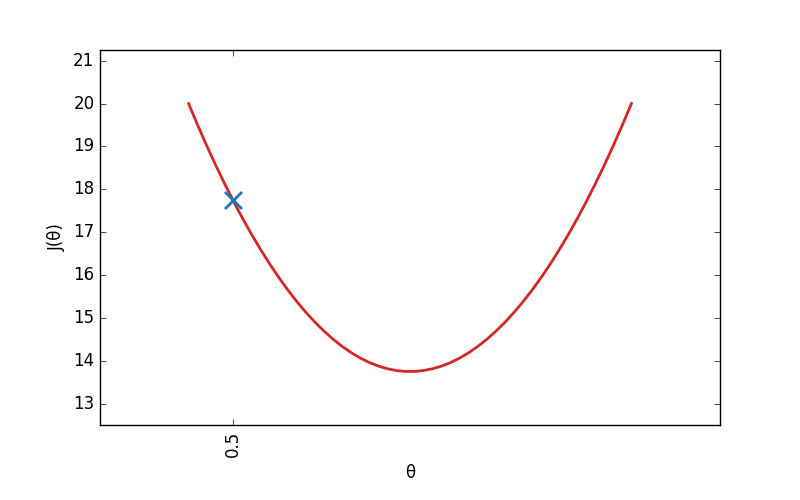
Ce que je veux faire, c'est modifier θ pour le rapprocher de sa bonne valeur. Est-ce que je dois augmenter θ ou au contraire le diminuer ? Pour le savoir, il me suffit de regarder la courbe de la fonction J. Si J descends, c'est qu'il faut augmenter θ pour se rapprocher du minimum de J. Si au contraire, J monte, c'est qu'il faut diminuer θ.

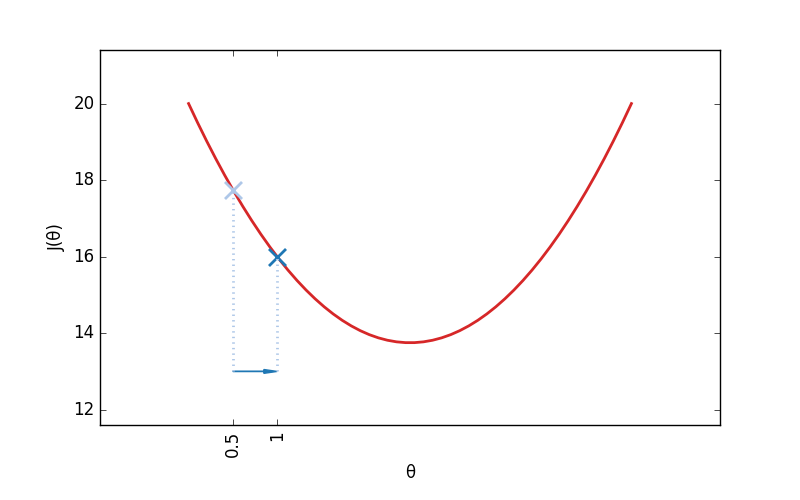
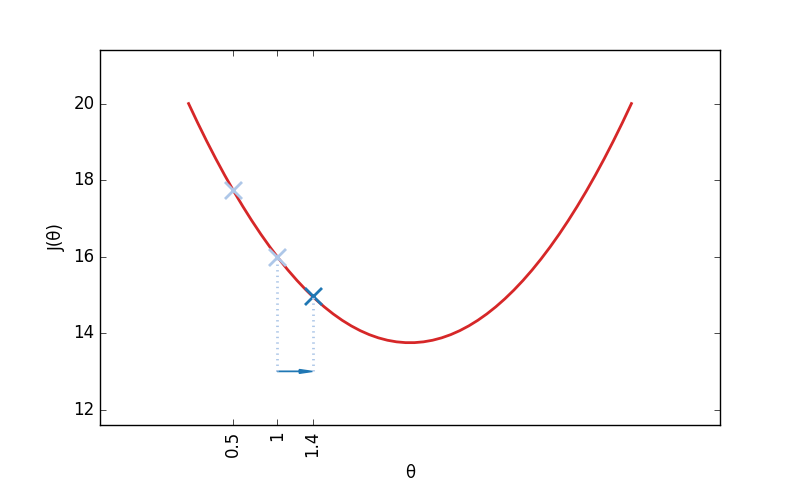
Je vais ainsi procéder par petites étapes successives. Calculer si, pour une valeur donnée de θ, J croit ou au contraire décroit, et légèrement modifier θ en conséquence. Au bout d'un certain nombre d'étapes, on atteint forcément la valeur optimale de θ, on a donc terminé l'entraînement du modèle.

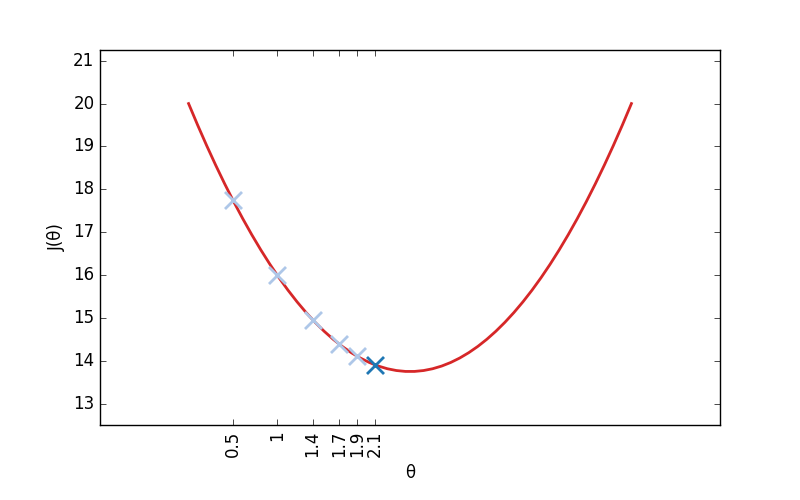
Et mais ?! Attends un peu !? Comment peut-on déterminer la pente de J ? Et bien, si vous vous souvenez de vos cours de maths, c'est justement le rôle de la fonction dérivée (qu'on note généralement J'). Calculer J' la dérivée de J, c'est calculer la fonction qui nous permet de calculer la pente de J.

On peut en conclure que l'algorithme précédent peut-être décrit par le pseudo-code suivant :

initialiser θ à une valeur aléatoire
répéter jusqu'à ce que θ converge:
    θ <- θ - α * J'(θ)

Ou α est une valeur constante à définir au préalable, qui correspond à la vitesse à laquelle on déplace θ.

Que se passe-t-il ici ?

• Si J(θ) a une pente fortement montante, il y a des chances pour qu'on soit très loin à droite du minimal de J. Et comme J'(θ) sera très positif, on va réduire θ très fortement.
• Si J(θ) a une pente légèrement montante, il y a des chances pour qu'on soit assez proche à droite du minimal de J. Et comme J'(θ) sera faiblement positif, on va réduire θ d'un petit chouilla.
• Si J(θ) a une pente fortement descendante, il y a des chances pour qu'on soit très loin à gauche du minimal de J. Et comme J'(θ) sera très négatif, on va augmenter θ très fortement.
• Si J(θ) a une pente légèrement descendante, il y a des chances pour qu'on soit assez proche à gauche du minimal de J. Et comme J'(θ) sera faiblement négatif, on va augmenter θ d'un petit chouilla.

Honnêtement, à ce stade, je ne sais pas du tout si je m'exprime clairement ou si je suis aussi cohérent qu'un cadre du FN expliquant le programme économique de son parti la bouche pleine de galette.

Vous je ne sais pas, mais quand j'ai découvert cet algorithme (qui porte le doux nom d'algorithme du gradient descendant), qui permet d'accomplir une tâche aussi complexe d'une manière aussi simple, j'ai eu la petite larme à l'œil. Qu'on essaye encore de me faire croire que les mathématiques ne relèvent pas de la magie pure.

Oui, mais bon, que se passe-t-il si J prends non pas un mais deux paramètres ? le mécanisme reste le même, mis à part le fait que la représentation de J nécessite un format 3d.

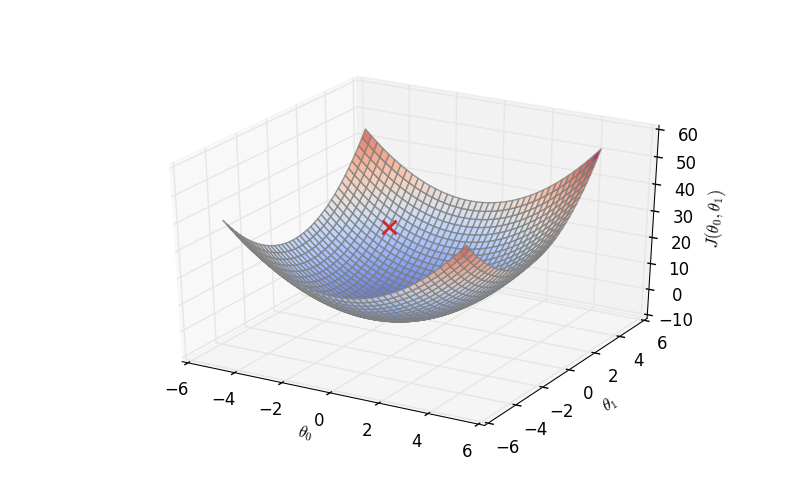
J peut prendre un nombre infini de paramètres, le mécanisme reste le même, même s'il devient impossible de représenter la fonction visuellement.

Du code bordel !

Du code vous voulez, du code vous aurez.

Voici le code qui implémente l'algorithme du gradient, indépendamment de tout mécanisme d'affichage.

// Quelle est la valeur calculée par un modèle donné ?
//
// theta est un tableau qui contient la liste des paramètres θ
var hypothesis = function(x, theta) {
    return theta[0] + theta[1] * x;
};


// Fait tourner une seule itération de l'algorithme du gradient
//
// x est un tableau qui contient nos données d'entrée (les surfaces)
// y est un tableau qui contient les réponses attendues (le montant des loyers)
// theta contient les paramètres actuels de notre modèle.
var run_gradient_descent = function(x, y, theta) {
    var learning_rate = 0.0001;
    var m = y.length;  // m = le nombre d'exemple dans nos données d'apprentissage
    var new_theta = [];

    // Mise à jour de chaque paramètre theta tour à tour
    for (var i_theta = 0 ; i_theta < theta.length ; i_theta++) {

        // Calcul de la dérivée partielle de la fonction J en fonction de θ[i_theta]
        var errors = 0;
        for (var i = 0 ; i < m ; i++) {
            if (i_theta == 0) {
                errors += (hypothesis(x[i], theta) - y[i]);
            } else {
                errors += (hypothesis(x[i], theta) - y[i]) * x[i];
            }
        }
        errors /= m;

        // Mise a jour du paramètre theta en multipliant le taux
        // d'apprentissage (α) et la dérivée J'
        new_theta[i_theta] = theta[i_theta] - learning_rate * errors;
    }
    return new_theta;
};

// Ici, on pourrait initialiser θ aléatoirement, mais je suis tellement
// fainéant que je vais juste mettre zéro partout.
var theta = [0, 0];
for (var i = 0 ; i < NB_ITERATIONS ; i++) {
    theta = run_gradient_descent(x, y, theta);
}

Le plus beau dans cette histoire, c'est que l'algorithme du gradient ne dépend absolument pas du modèle : vous pouvez expérimenter diverses fonctions sans vous fatiguer.

Notez que cette implémentation est hautement inefficace. À ne jamais utiliser telle quelle, bien entendu.

Jouons un peu

Utilisez les boutons pour faire tourner quelques itérations de l'algorithme du gradient et constatez qu'à chaque étape, notre modèle se rapproche un petit peu de sa valeur optimale.

Vous constaterez que les différents paramètres θ ne convergent pas à la même vitesse. C'est parce qu'ils sont d'ordres de grandeur différents, un problème que nous aurions pu régler en pré-traitant nos données.

Conclusion

Que pouvons nous retirer de cette petite étude ?

D'abord, faute de disposer d'autres paramètres, on peut estimer le loyer d'un logement d'une surface x à Montpellier par la formule suivante : h(x) = 223 + 7x (prix de 2015, of course).

Mais ça, on s'en fout. Qu'avons nous appris sur le machine learning ?

D'abord, face à un problème donné, nous avons vu les étapes à mettre en place pour la création d'un premier prototype.

Aller plus loin nécessitera d'itérer, pour trouver si possible un meilleur modèle. Pour ce faire, il nous faudra calculer des métriques de pertinence, séparer nos données en un jeu d'apprentissage et un jeu de test de pertinence, évaluer les paramètres du modèle et si possible en ajouter, bref ! tous les petits raffinements qui séparent un prototype d'un vrai MVP.

En revanche, quelque soit la complexité du modèle choisi, le processus ne changera que peu.

Mais ceci… est une autre histoire !

Edit : la suite est ici.