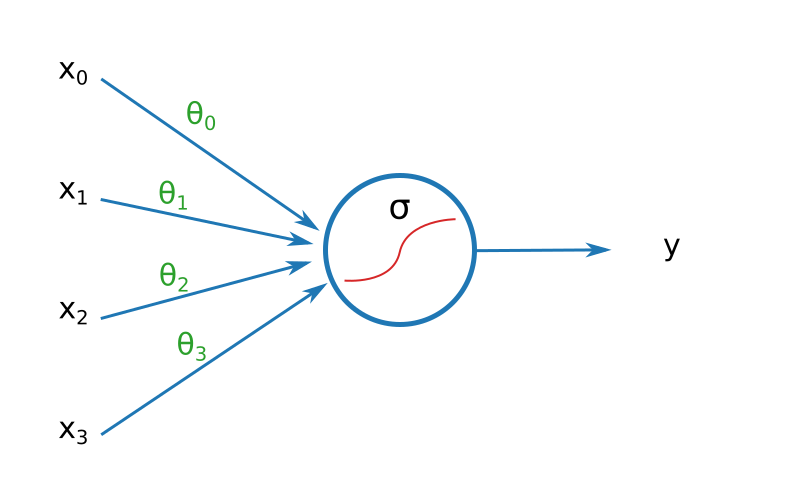
Machine learning : la régression logistique
« Alors détective ! On a encore oublié son imper ?! ».

Trempé jusqu'aux os, la pluie glacée ruisselant le long de mes chevilles pour venir imbiber mes chaussettes trouées, je maudis silencieusement le kiosquier du bas de la grand rue Jean Moulin qui venait de griller ma couverture. « Que l'e-vérole emporte tous tes périphériques ! » grinçais-je entre les dents.
La poisse me collait au train comme la confiture d'abricots maison aux doigts d'un marmot pas sage. D'abord, il y avait eu ce client tellement déconfit du résultat de la filature qu'il avait refusé en bloc de s'acquitter de la facture — comme si j'étais responsable des agissements de sa femme, secrètement bénévole à la Croix-Rouge au lieu de se rendre tous les mardis à ses prétendues compétitions de bridge. Ensuite, ma vieille guimbarde avait décidé qu'il était temps pour elle de vérifier si les machines pouvaient accéder au cycle de réincarnation. Et maintenant, les éléments. Crotte et flûte !
Le b.a.-ba de la filature, c'est de ne pas attirer l'attention. Et s'il est difficile de ne pas passer pour un taré en se baladant en imper un jour de grand Soleil, vous n'aurez pas l'air plus malin en tentant de déambuler innocemment en bras de chemise sous une averse.
Bref ! Imper ou pas imper ? Telle est l'interrogation quotidienne de n'importe quel privé, et la première décision d'une longue liste qui aboutira à une filature réussie ou un fiasco navrant.
Grillé, trempé, dépité, je décidai d'arrêter le massacre et regagnai mes pénates en maugréant. Le dilemme de l'imper m'avait bousillé une mission de trop, j'étais décidé à y remédier.
À peine rentré, j'envoyai valser mes chaussures trempées, rallumai la cafetière pour réchauffer le reste de précieux breuvage, et poussai le radiateur à fond — tant pis pour la note d'électricité que de toutes manières je ne pourrais pas payer ce mois-ci.
Ces derniers temps, j'avais passé mes — trop nombreuses — heures de temps libre à prendre des cours en ligne sur le machine learning, un ensemble de techniques permettant d'apprendre à son ordinateur à résoudre ses problèmes à sa place – une technologie de fainéant, en sommes. J'avais déjà utilisé ces outils pour confirmer ce que je soupçonnais déjà : je payais bien trop cher pour mon petit local aux murs noircis de fumée.
J'ouvris le cahier dans lequel j'avais griffonné des notes plus ou moins lisibles et décidai de commencer par le commencement. Avant toutes choses, il me fallait formaliser le problème, car rien ne sert de commencer une réparation avant d'avoir trouvé la panne. Je voulais une méthode simple me permettant de décider, sur une base concrète, si je devais embarquer mon imper ou pas avant une filature. Ce qui revenait à se poser la plus vieille question du monde : va-t-il pleuvoir ou pas ?
Il me fallait ensuite déterminer un modèle approprié. Honnêtement, je déteste les scientifiques : non content d'employer à tire-larigot des symboles difficiles à saisir et pratiquement impossibles à indexer dans les moteurs de recherche — comme « θ », « σ » ou « ε » —, ils ne manquent pas une occasion d'utiliser un même terme pour désigner un peu tout et n'importe quoi. Je m'étais arraché beaucoup des quelques cheveux n'ayant pas encore déserté pour essayer de comprendre cette injonction « imaginez un modèle adapté à la résolution du problème ». J'en étais arrivé à la conclusion qu'un « modèle de données » pouvait se comprendre par une « traduction des données dans une forme — n'importe laquelle on s'en fout — utilisable, par exemple une grosse équation ou une bête fonction python ou javascript ». Pas très formel, mais compréhensible.
Indifférent à l'odeur de café brûlé se répandant dans la pièce, je m'absorbais dans mes pensées. Quels étaient les indicateurs à ma disposition ? D'abord, il y avait la petite station météo locale, qui publiait chaque jour un indice (de 1 à 50) indiquant le risque de pluie. Je savais toutefois que leur matériel n'était pas du dernier cri — la faute aux habituelles coupes budgétaires — et leurs prévisions pas toujours fiables.
Ensuite, il y avait ma blessure. Je trimballais depuis quelques années une fracture de la clavicule qui ne s'était jamais parfaitement ressoudée. Lorsqu'on me posait la question, je prenais des airs ténébreux pour ne pas être obligé d'avouer qu'elle résultait d'une chute de poney, et je priais pour ne jamais avoir à conter cette navrante anecdote. Toujours est-il qu'elle me faisait parfois souffrir en période d'humidité, et tout bien réfléchi, ce n'était pas un indicateur plus bête qu'un autre.
Enfin, il y avait le perroquet de mamie Jacquotte, la vieille folle du cinquième. J'avais remarqué que j'entendais mieux les piaillements de l'oiseau saugrenu lorsqu'il allait faire beau, et j'en avais conçu l'étrange superstition que le volatile disposait d'un sixième sens pour prévoir la pluie.
J'avais l'entrée de mon modèle ! Trois indicateurs. Je n'avais aucune idée de leur fiabilité, mais je n'allais pas tarder à le découvrir ! Et en sortie ? Facile, je ne désirais qu'une chose, un nombre entre zéro et un, pour indiquer la probabilité de pluie.
Voici à quoi ressemblait mon modèle, une simple fonction à trois paramètres renvoyant un nombre flottant entre 0 et 1 :
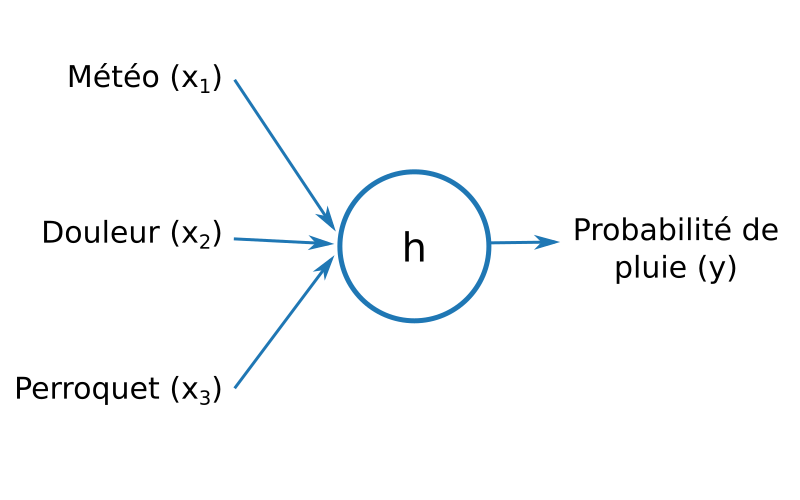
Pour respecter les notations en vigueur, je notai x1, x2 et x3 les trois variables en entrée, et y le résultat obtenu. Je nommai mon modèle h. Pour faciliter les notations, je regroupai les trois entrées en un seul tableau (ou vecteur, pour les mathématiciens).
$$ x = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} $$
Il me fallait maintenant déterminer le contenu exact de la fonction h. Instinctivement, je me doutais que les différents critères à ma disposition n'avaient pas tous la même fiabilité, néanmoins, j'ignorais dans quelle mesure exactement chaque donnée devait être prise en compte pour savoir si je devais me munir de mon imperméable ou au contraire, rester à découvert. Par exemple, j'imaginai que plus ma clavicule me faisait mal, plus la probabilité de pluie augmentait ; toutefois, une absence de douleur n'était peut-être pas significative si la station météo estimait que les chances de précipitations étaient importantes.
Je décidai de respecter l'usage qui consistait à multiplier chaque variable par un « poids » spécifique, dont les valeurs seraient à déterminer plus tard. Les différents poids seraient nommés θ1 (thêta), θ2… ce qui me permettait de définir une fonction g ainsi :
$$g_\theta(x) = \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_3$$
J'introduisis également un « biais », un poids indépendant de toutes les variables, afin de permettre une configuration du modèle la plus précise possible. Pour faciliter différentes notations, j'ajoutais une nouvelle variable d'entrée « x0 » = 1 fictive, ce qui me donnait la formule suivante :
$$g_\theta(x) = \theta_0 x_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_3$$
Comme tout à l'heure, je regroupai les différentes variables en un seul vecteur θ :
$$ \theta = \begin{pmatrix} \theta_0 \\ \theta_1 \\ \vdots \\ \theta_n \end{pmatrix} $$
Amusé, je me rendis compte qu'il était possible de simplifier énormément cette notation.
$$g_\theta(x) = \theta_0 x_0 + \theta_1 x_1 + ... + \theta_n x_n = \sum_{i=0}^{n} (\theta_i x_i) = \theta \bullet x$$
Où le symbole « ∙ » désigne le produit scalaire.
Songeur, je m'arrêtai un instant en mâchonnant mon stylo, inconscient de la goutte d'encre qui se répandait sur mon menton pour venir tâcher mon col de chemise. Un tel modèle était typique d'un problème de régression linéaire : à plusieurs variables explicatives, il faisait correspondre une valeur comprise entre moins l'infini et plus l'infini. Toutefois, je souhaitais obtenir une valeur comprises entre zéro et un. Il manquait quelque chose, une moulinette dans laquelle passer le résultat de ma formule pour le ramener à une valeur utile. Je me replongeai dans mes notes à la recherche d'une fonction adaptée.
Eurêka ! Ce qu'il me fallait, c'était la Sigmoïde ! Pardon, vous ne connaissez pas la fonction Sigmoïde ? C'est pourtant l'une des rares fonctions à bien porter son nom, puisque « sigmoïde » signifie « en forme de "s" ».
Sa définition est la suivante (« σ » se lit « sigma ») :
$$\sigma(x) = \frac{1}{1 + e^{-x}}$$
Et voici sa représentation :
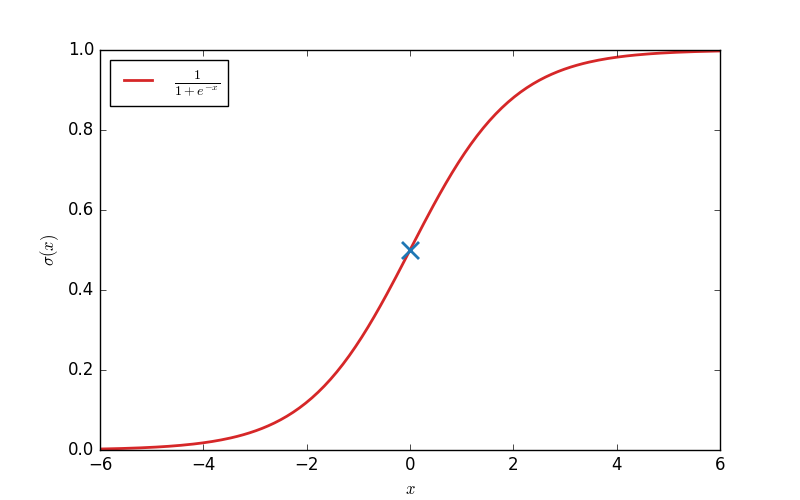
Je ne pus m'empêcher de jubiler en constatant à quel point cette fonction allait m'être utile. L'avantage de la fonction Sigmoïde, c'est que σ(x) tend vers 1 quand x tend vers l'infini, et vers 0 quand x tend vers moins l'infini.
$$\begin{array}{ll} \lim\limits_{x \to +\infty}\sigma(x) = 1\\ \lim\limits_{x \to -\infty}\sigma(x) = 0 \end{array}$$
Autre constat utile : σ(0) = 0.5. Ce qui signifie que σ(x) > 0.5 quand x > 0, et σ(x) < 0.5 quand x < 0. Par conséquent, je pouvais définir mon modèle final sous cette forme :
$$h_\theta(x) = \sigma(g_\theta(x)) = \frac{1}{1 + e^{-\theta \bullet x}}$$
Ainsi, mon modèle aurait les propriétés suivantes :
- si toutes mes variables en entrée sont petites (pas de douleur, pas de chant du perroquet, prévision de pluie faible), alors gθ(x) sera petit, et hθ(x) sera proche de zéro : pas besoin de prendre mon imper ;
- à l'inverse, si toutes mes variables sont élevées, alors gθ(x) sera grand, et hθ sera proche de un : mieux vaut emporter l'imper ;
- si gθ(x) tend vers zéro, alors hθ(x) tend vers 0.5 : les chances de pluies ou beau temps sont de 50 / 50.
Je jetai un coup d'œil à mon modèle. Pas de doutes, ça avait de la gueule !
Amusé, je songeai que tout cela ressemblait furieusement aux illustrations de mes anciens manuels de SVT, quand le vieux M. X essayait de nous inculquer le fonctionnement du cerveau alors que lui-même en était visiblement totalement dépourvu. Tout ce que j'avais à faire, c'est trouver les bonnes valeurs de θ au moyen d'un algorithme d'apprentissage.
Je décidai d'accorder quelques instants de répit à mes neurones en surchauffe. Je versai dans l'évier empli de vaisselle sale le liquide boueux qui avait été du café avant de préparer une nouvelle fournée, m'enjoignant mentalement à ne pas oublier d'en boire cette fois-ci. Je profitai du glougloutement apaisant de la cafetière agonisante pour laisser dériver mes pensées vers les étapes suivantes de mon projet.
Qui dit algorithme d'apprentissage dit… données ! Et des données, heureusement, j'en avais ! Je me félicitai intérieurement d'avoir cédé à la mode ridicule du quantified self quelques mois auparavant : j'avais pris l'habitude quotidienne de noter quelques métriques et faits marquants sur ma journée avant de m'endormir ; rien de tel que de griffonner des platitudes pour trouver le sommeil ! Soufflant la poussière de cartons tirés de sous mon lit, je m'emparai de dizaines de cahiers que j'avais noirci d'une écriture brouillonne et me plongeai dans mes archives personnelles. Après avoir patiemment exhumé les informations utiles au milieu de souvenirs parfois pénibles, souvent barbants, j'obtins un tableau avec, je l'espérais, suffisamment d'infos pour nourrir un algorithme d'apprentissage.
| x0 | x1 | x2 | x3 | y |
|---|---|---|---|---|
| 1 | 50 | 2 | 10 | 1 |
| 1 | 15 | 1 | 2 | 0 |
| 1 | 7 | 5 | 2 | 1 |
| 1 | 3 | 3 | 10 | 0 |
| … | ||||
| 1 | 8 | 5 | 7 | 1 |
Il manquait quelque chose, toutefois ! Un peu de pré-traitement. Car si l'état déplorable de mon petit bureau m'avait parfois valu le sobriquet d'« agent des forces du désordre » de la part d'amis taquins, j'étais en revanche obsessivement tatillon dés qu'il s'agissait du boulot.
J'avais appris que pour un fonctionnement efficace de l'algorithme d'apprentissage, mieux valait que les données d'entrées soient du même ordre de grandeur. Qu'à cela ne tienne, il suffisait de considérer chaque colonne, diviser par la valeur maximum et vous obteniez des valeurs dans l'intervalle [0, 1].
Après cette étape de nettoyage, mes données ressemblaient à ça :
| x0 | x1 | x2 | x3 | y |
|---|---|---|---|---|
| … | ||||
| 1 | 0.367 | 0.2 | 0.6 | 0 |
| 1 | 0.122 | 0.3 | 0.6 | 0 |
| 1 | 0.816 | 0.8 | 0.6 | 1 |
| 1 | 0.735 | 0.7 | 0.6 | 1 |
| … | ||||
| 1 | 1.000 | 0.1 | 0.8 | 1 |
J'en profitai pour griffonner sur une feuille tâchée quelques éléments de notation en guise de pense-bête. C'est qu'il y avait beaucoup de variables à considérer, et j'avais tendance à facilement m'emmêler les pinceaux.
- hθ ou simplement h représente la fonction qui correspond au modèle. On trouve parfois la notation h(x;θ).
- m est le nombre d'exemples disponible pour l'apprentissage. J'avais péniblement rempli 450 lignes dans mon tableau, donc m = 450.
- n est le nombre de paramètres passés à la fonction hθ, c'est à dire le nombre de caractéristiques possédées par chaque entrée dans le jeu de test. Ici, je considérais trois informations plus un biais, j'avais donc n = 3 (car l'index commence à zéro).
- θ (thêta) est le vecteur qui contient l'ensemble des paramètres θ0, θ1… du modèle, c'est à dire les nombres que je m'apprêtais à ajuster.
$$ \theta = \begin{pmatrix} \theta_0 \\ \theta_1 \\ \vdots \\ \theta_n \end{pmatrix} $$
- x(i) est le iième exemple des données de test, c'est à dire un vecteur contenant 4 éléments correspondants aux valeurs x0, x1… de la iième ligne du tableau.
- xj(i) est la valeur de la jième variable de la iième ligne du tableau.
- X est la matrice qui contient l'ensemble des données de test. C'est une matrice de dimension (m, n), c'est à dire à m lignes et n colonnes.
$$ X = \begin{pmatrix} - & x^{(1)} & - \\ - & x^{(2)} & - \\ & \vdots & \\ - & x^{(m)} & - \end{pmatrix} = \begin{pmatrix} x_0^{(1)} & x_1^{(1)} & x_2^{(1)} & ... & x_n^{(1)} \\ x_0^{(2)} & x_1^{(2)} & x_2^{(2)} & ... & x_n^{(2)} \\ \tiny{\vdots} & & & \tiny{\ddots} \\ x_0^{(m)} & x_1^{(m)} & x_2^{(m)} & ... & x_n^{(m)} \end{pmatrix} $$
- y(i) est le résultat obtenu pour le iième exemple. 0 = il n'a pas plu ce jour là, 1 = il a plu.
- y est le vecteur qui contient la liste des résultats attendus pour les données d'entrée.
$$ y = \begin{pmatrix} y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(m)} \\ \end{pmatrix} $$
Pfiu ! Ça faisait pas mal d'informations à conserver à l'esprit.
J'étirai les bras en baillant et gémis de contentement lorsqu'un craquement témoigna d'un soudain dégrippage de quelque vertèbre. Ça y était presque ! Il ne me restait plus qu'à implémenter l'algorithme du gradient descendant pour obtenir les valeurs de θ et ainsi obtenir un modèle fonctionnel. Je fouillai mes notes pour retrouver le pseudo-code.
Initialiser θ à une valeur aléatoire
Répéter jusqu'à ce que θ converge:
θ ← θ - α * J'(θ)
Bigre ! encore de nouvelles variables grecques… Je m'étalai de l'encre sur le front en me grattant le crâne, tâchant d'en rappeler la signification. J'étais lancé, le souvenir revint sans trop de difficulté. α (alpha) était le « taux d'apprentissage » : une constante à spécifier au préalable qui permettait de configurer la vitesse à laquelle θ allait varier. Tout ce que j'avais retenu, c'était que si α était trop petit, l'apprentissage prenait plus de temps que nécessaire alors que s'il était trop grand, l'algorithme pouvait carrément ne pas converger. Il suffisait de trouver la bonne valeur par tâtonnement, en prenant une valeur de départ comme 0.03, par exemple.
Quand à J'(θ), c'était la dérivée de la fonction de coût. Celle là, je l'avais complètement oublié. Elle est pourtant essentielle : c'est elle qui permet de mesurer la pertinence d'un modèle, et donc de guider l'algorithme d'apprentissage.
Lors d'un précédent exercice, j'avais appris qu'on pouvait utiliser l'erreur quadratique moyenne en guise de fonction de coût. Les origines et justification statistiques de ce choix m'avaient fait tourner la tête, mais l'explication était relativement intuitive. Vous preniez un modèle θ et une hypothèse hθ, passiez en entrée des données x de votre tableau d'apprentissage pour lesquelles vous connaissiez déjà le résultat y, et calculiez la différence entre les deux : hθ(x) - y. Plus la différence était importante, plus votre modèle était à côté de la plaque. En calculant la moyenne des carrés des erreurs, vous obteniez une bonne estimation de la pertinence de votre modèle.
Seulement voilà, le prof qui avait l'air de savoir de quoi il parlait avait expliqué que cette fonction n'était pas pertinente dans le cas d'une régression logistique, ce qui apparemment était le nom de la technique que j'étais en train de mettre en œuvre. La chose était fort bien expliquée, mais je décidai que j'avais bien assez de choses à comprendre et décidai de remettre à plus tard l'étude de ses raisons. Dans la même optique, j'adoptai bêtement la nouvelle fonction de coût J(θ) proposée :
$$J(\theta) = -\frac{1}{m} \sum_{i=1}^{m} [(y^{(i)}log(h_\theta(x^{(i)})) + (1-y^{(i)})log(1-h_\theta(x^{(i)}))] _\enspace$$
Cette fonction d'apparence indigeste n'était utilisable que dans le cas ou y pouvait prendre une valeur discrète {0, 1}. Il fallait un peu de temps pour en comprendre l'utilité et surtout la beauté, mais l'avantage était qu'il n'y avait pas besoin de la comprendre pour l'implémenter, raccourci que j'allais m'empresser d'emprunter.
J'acceptai pareillement sans réfléchir la définition de la dérivée partielle de J par rapport à chaque paramètre θj :
$$\frac{\partial}{\partial \theta_j} J(\theta) = \frac{1}{m} \sum_{i=1}^{m}(h_\theta(x^{(i)})- y^{(i)})x_j^{(i)}$$
J'avoue que cette équation avait provoqué plus d'une migraine et était responsable de la chute vertigineuse de mon stock de bon bourbon. Je me souvenais des propos de Mme. Y, ma prof de maths en terminale S : « Un jour, Monsieur J., vous regretterez de ne pas avoir écouté mes explications sur la signification des dérivées partielles ». J'avais écopé de deux heures de colle pour lui avoir ri au nez. Si j'avais su ! L'heure de l'apéro approchant à grands pas, je décidai de me verser un verre de Scotch pour le boire à sa santé. Elle était décédée deux ans plus tôt, à peine trois mois après son départ en retraite, de complications suite à une crise de calculs. Un comble pour une prof de maths !
Toute nostalgie mise à part, j'avais dû sacrément me rafraîchir la mémoire sur les notions de calcul différentiel. Le concept de dérivation de fonction, ça, je maîtrisais à peu près. Si la dérivée f' est positive en un point x, c'est que f est croissante à cet endroit, si f' est négative, c'est que f est décroissante. Pour calculer f', il suffit d'appliquer bêtement quelques formules. Facile.
J'avais ensuite étudié la notion de dérivée partielle. Ce n'était finalement pas beaucoup plus compliqué : quand on avait une fonction à plusieurs variables, on calculait la dérivée partielle par rapport à l'une des variables en prétendant que toutes les autres étaient des constantes avant d'appliquer les formules mentionnées plus haut.
Par exemple, si on avait une fonction f(x1, x2, x3), donc à trois paramètres, on pouvait calculer trois dérivées partielles.
Qu'est-ce que cela signifiait dans mon cas ? J'avais une fonction de coût J(θ) avec θ = θ0, θ1… θn, donc n + 1 paramètres. Calculer la dérivée partielle de J par rapport à θ0, par exemple, me permettait de savoir dans quelle direction modifier θ0 pour diminuer globalement J(θ), comme je l'avais fait lorsque J ne prenait qu'un seul paramètre.
Cette fois, j'étais paré ! J'avais mes données, ma fonction de coût, mes algorithmes ! Il ne manquait plus que le code. Je lançai mon éditeur préféré d'un raccourci bien sentit, et hésitai une fraction de seconde. En quel langage implémenter mon modèle ? Certes, en Python, j'aurais pu bénéficier de librairies optimisées telles que scikit-learn ou NumPy pour une implémentation à hautes performances. D'un autre côté, avec un modèle aussi simple et un jeu de données aussi réduit, n'importe quel langage ferait l'affaire. Je me décidai donc pour une implémentation en Javascript, afin de dérouiller un peu mes compétences dans ce langage.
// Implémente la fonction logistique ou sigmoide
var sigmoid = function(x) {
return 1 / (1 + Math.exp(-x));
}
// Calcule le produit vectoriel de deux tableaux
var dot = function(a1, a2) {
if (a1.length !== a2.length) {
throw 'Both arrays must have the same length';
}
var sum = 0;
for (var i = 0 ; i < a1.length ; i++) {
sum += a1[i] * a2[i];
}
return sum;
}
// Implémente l'hypothèse pour transformer les données en proba pluie / non pluie
var hypothesis = function(x, theta) {
return sigmoid(dot(x, theta));
};
// La fonction de coût
var J = function(X, y, theta) {
var n = theta.length;
var m = X.length;
var errors = X.map(function(x, i) {
return y[i] * Math.log(hypothesis(x, theta)) + (1 - y[i]) * Math.log(1 - hypothesis(x, theta));
});
var error_sum = errors.reduce(function(a, b) { return a + b; });
return -error_sum / m;
}
C'était tellement facile ! Tout était sur le papier, il suffisait de recopier. Du véritable pissage de code. J'attaquai l'algorithme d'apprentissage, même pas plus complexe.
// Joue une seule itération de l'algo du gradient descendant
//
// Mise à jour des paramètres theta grâce au calcul des dérivées partielles
var run_gradient_descent = function(X, y, theta) {
var learning_rate = 1;
var m = y.length;
var new_theta = [];
// Pour chaque paramètre theta
for (var j = 0 ; j < theta.length ; j++) {
// Calcul de la dérivée partielle de la fonction de coût
var errors = 0;
for (var i = 0 ; i < m ; i++) {
errors += (hypothesis(X[i], theta) - y[i]) * X[i][j];
}
errors /= m;
// Et mise à jour de theta
new_theta[j] = theta[j] - learning_rate * errors;
}
return new_theta;
};
C'était tout ! Mon modèle était là ! Il ne me restait plus qu'à implémenter un peu de code accessoire, histoire de charger les données, afficher la fonction de coût en fonction du nombre d'itération, ajouter une petite interface, etc. Cela ne me prit quelques minutes (c'est un euphémisme pour dire que toute ma nuit y est passée). Pour ce résultat :
Faut-il prendre l'imper ? (% de chances de pluie.)
Il était amusant de constater que θ étant initialisé aléatoirement, le modèle de départ était plus ou moins proche de la vérité et nécessitait plus ou moins d'itérations de l'algorithme d'apprentissage avant de devenir pertinent.
Je vérifiai également qu'avant de débuter l'entraînement, le modèle donnait des résultats complètement farfelus, alors qu'ils semblaient plutôt cohérent une fois l'algorithme exécuté.
Enfin, je constatai que les différents paramètres d'entrée n'avaient pas tous le même impact sur le résultat : le perroquet de mamie Jacquotte était finalement un élément de prévision pluviométrique peu fiable.
Épuisé, je me traînai jusqu'à mon lit, déroulant un fil d'Ariane constitué de vêtements abandonnés à même le sol, avant de m'écrouler de sommeil. Dans un dernier éclair de conscience, je m'abandonnai à la satisfaction puérile d'avoir mobilisé des technologies de pointe sur un problème vieux comme le monde. C'est beau la science !