Deep learning : la rétropropagation du gradient
Deuxième partie du notre tutoriel sur le deep learning, au cours duquel nous étudierons le fonctionnent d'un algorithme poètiquement intitulé la rétropropagation du gradient, ou backpropagation dans la langue de chat qu'expire.
Lors du précédent tutoriel, nous avons vu comment créer un modèle complexe basé sur un réseau de neurones. Un tel modèle est capable de réaliser des tâches intéressantes, comme la reconnaissance de l'écriture humaine, à condition d'être paramétré correctement.
À l'initialisation, les poids (et biais) du modèle reçoivent des valeurs aléatoires, ce qui le rend globalement inutile. Dans ce billet, nous allons voir comment un tel modèle peut être entraîné de manière efficace. Pour ce faire, nous implémenterons un algorithme intitulé l'algorithme de rétropropagation du gradient (je sais, ça claque !).
Cet algo constitue une importante pierre à poser pour se construire une bonne compréhension théorique du fonctionnement du deep learning. Il n'est pas essentiel de le comprendre — ou même de le connaître — pour implémenter du deep learning sur des cas concrets, mais un peu de culture générale ne fait jamais de mal.
Avertissement ! Si vous êtes allergique aux maths, prévoyez des antihistaminiques…
Rappel des épisodes précédents
Voici un rappel des épisodes précédents pour les gens distraits. Pour entraîner un modèle, il faut d'abord choisir une fonction de coût destinée à évaluer sa précision.
Nous avions l'habitude de noter cette fonction J(θ), mais nous adopterons une notation alternative : C(w, b). Il existe différentes fonctions traditionnellement utilisées dépendamment du contexte, ce qui pourrait constituer un billet à part entière. Il nous suffit de dire que peu importe la forme exacte de la fonction, les principes de base ne changent pas.
Nous avions également utilisé l'algorithme du gradient pour adapter les différents poids (et biais) afin de trouver itérativement un modèle qui minimise la fonction de coût. Pour ce faire, nous calculions la dérivée partielle de la fonction par rapport à chaque paramètre pour savoir dans quelle direction en modifier la valeur.
Rappel des notations utilisées
Voici un rappel des différentes notations utilisées pour décrire un réseau de neurones.
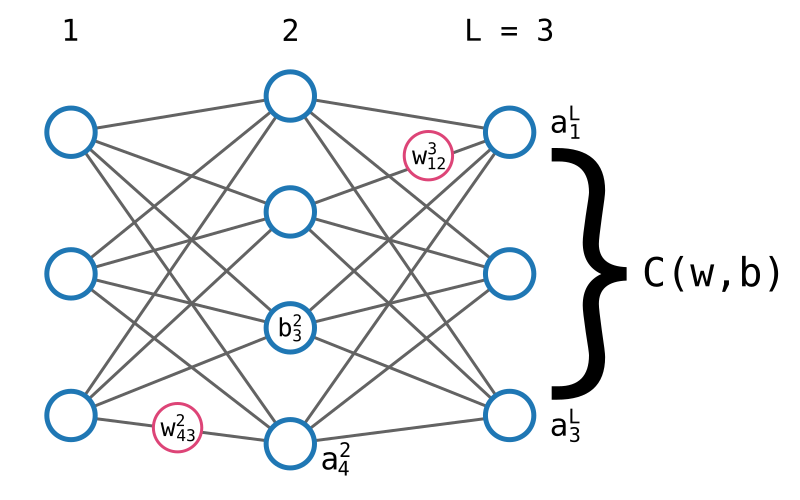
- L est le nombre de couches du neurones.
- \(\sigma\) est la fonction d'activation Sigmoïde.
- \(w^{l}_{ij}\) est le poids qui relie le iième neurone de la lième couche au jième neurone de la (l - 1)ième couche.
- \(w^l\) est une matrice de taille i x j (i lignes et j colonnes) qui contient tous les poids de la lième couche.
- \(b^l_i\) est le biais associé au iième neurone de la lième couche.
- \(b^l\) est le vecteur qui contient tous les biais de la lième couche.
Nous allons également introduire deux éléments de notation supplémentaires (oui, je sais, encore ! c'est la dernière fois, promis).
\(z^l_i\) est la valeur d'agrégation du iième neurone de la lième couche, c'est à dire la valeur qu'un neurone calcule avant de la passer à la fonction d'activation.
$$ z^l_i = \sum_{j=1}^{n} w^l_{ij} a^{l - 1}_j + b^l_i $$
\(a^l_i\) est la valeur d'activation du iième neurone de la lième couche, c'est à dire la valeur définitive crachée par le neurone. On a donc \(a^l_i = \sigma(z^l_i)\).
On utilise bien évidemment une notation vectorielle qui permet de regrouper toutes les valeurs z et a d'une seule couche en une seule variable :
$$ z^l = \begin{pmatrix} z^l_1 \\ z^l_2 \\ \vdots \\ z^l_n \end{pmatrix} a^l = \begin{pmatrix} a^l_1 \\ a^l_2 \\ \vdots \\ a^l_n \end{pmatrix} $$
Dans le billet précédent, nous avons vu qu'il était possible de calculer ces valeurs ainsi :
$$ \begin{array}{l} z^l = w^l * a^{l - 1} + b^l \\ a^l = \sigma(z^l) \end{array} $$
L'algorithme de la rétropropagation du gradient
À ce stade, nous n'avons fait que rappeler des concepts déjà exposés et des éléments de notation. S'il y a le moindre truc que vous ne comprenez pas dans ce qui précède, si vous ne sentez pas familier avec les concepts de l'algo du gradient ou des dérivées partielles de fonction de coût, relisez les billets précédents avant de poursuivre, sous peine d'être complètement largué·e·s.
Nous pouvons maintenant entrer dans le vif du sujet (enfin) et aborder le fonctionnement de l'algorithme d'apprentissage dans un réseau de neurones.
À quelques subtilités près, entraîner un réseau de neurones fonctionne exactement sur le même principe que pour les modèles plus simples : répéter jusqu'à ce que C(w, b) converge, pour tous les poids \(w^l_{ij}\) et biais \(b^l_{i}\) :
$$ w^l_{ij} \leftarrow w^l_{ij} - \alpha * \frac{\partial C}{\partial w^l_{ij}} $$
$$ b^l_{i} \leftarrow b^l_{i} - \alpha * \frac{\partial C}{\partial b^l_{i}} $$
Ou α est le taux d'apprentissage.
Cet algorithme, l'algorithme du gradient, est ce que nous avons utilisé dans les précédents billets. Si l'algorithme ne change pas, alors quoi ? Et bien ! la seule difficulté, ici, réside dans le calcul des différentes dérivées partielles \(\partial C / \partial w^l_{ij}\) et \(\partial C / \partial b^l_{i}\).
En effet, comment calcule-t-on ces dérivées partielles ? Comment faire pour obtenir (par exemple) cette valeur :
$$ \frac{\partial C}{\partial w^2_{43}} $$
(Prononcer « d ronde de C sur d ronde de w bla bla bla ».)
D'habitude, si la fonction est simple, il suffit d'appliquer les règles de dérivation en s'aidant de quelques dérivées usuelles pour obtenir une dérivée en bonne et due forme.
Or, un réseau de neurones — modèle constitué de potentiellement millions de fonctions composées entres elles — n'est pas une fonction simple. Il faut trouver une autre solution.
Il existe heureusement une solution qui porte le doux nom d'algorithme de rétropropagation de gradient (backpropagation en angliche).
Avant d'étudier l'algo en détail, commençons par essayer de comprendre son fonctionnement de manière intuitive.
Rétropropagation du gradient : intuition
Imaginons une donnée d'entraînement (X, T) avec X le vecteur qui contient les entrées, et T (pour target) la sortie attendue.
Donnons X à notre réseau de neurones. Les calculs se propagent de couche en couche jusqu'à la sortie qu'on notera Y.
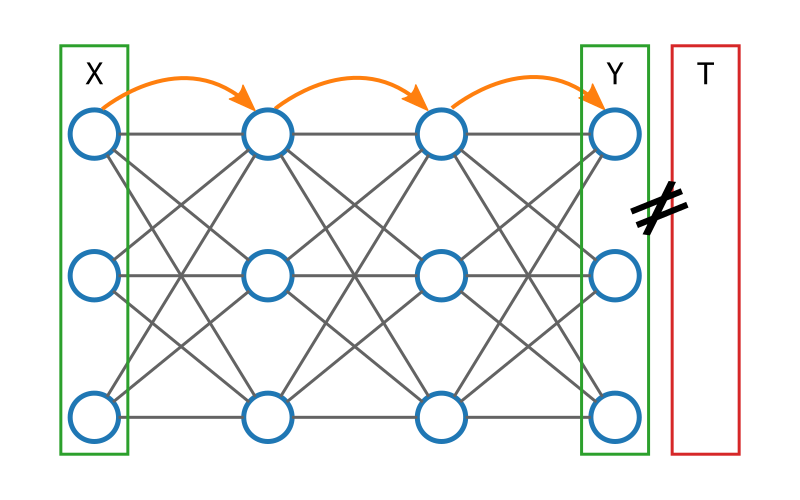
Si notre réseau n'est pas entraîné, il y a des chances pour que Y et T soient différents. Nous pouvons calculer très simplement l'erreur du modèle par l'équation suivante : E = T - Y (on note parfois E : δ). Par exemple :
$$ T = \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix} Y = \begin{pmatrix} 1 \\ 0 \\ 0.5 \end{pmatrix} E = T - Y = \begin{pmatrix} 0 \\ 1 \\ -0.5 \end{pmatrix} $$
Puisque nous connaissons la valeur attendue pour les neurones de la dernière couche, il est assez facile de savoir dans quelles mesures les poids associés à chaque neurone ont contribué à cette erreur. C'est à dire qu'il existe une formule (que nous verrons en détails plus loin) pour obtenir toutes les valeurs \(\partial C / \partial w^L_{ij}\) à partir de \(\delta^L\).
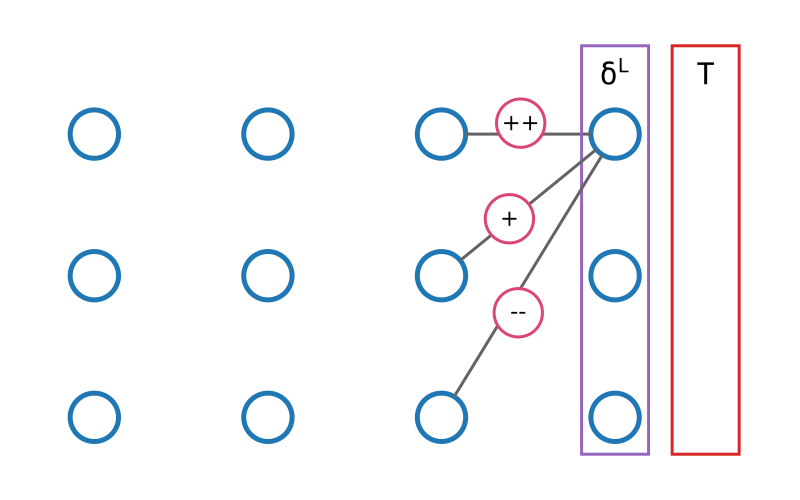
Nous connaissons la valeur attendue de la dernière couche, et nous savons quels
calculs ont permis de passer de l'avant-dernière à la dernière couche. Par
conséquent, il nous est possible, grâce à la magie d'astucieuses
opérations que nous verrons plus en détails ensuite, de calculer dans quelle
mesure les neurones de l'avant-dernière couche ont contribué à l'erreur. En
gros, nous pouvons calculer l'erreur de l'avant-dernière couche.
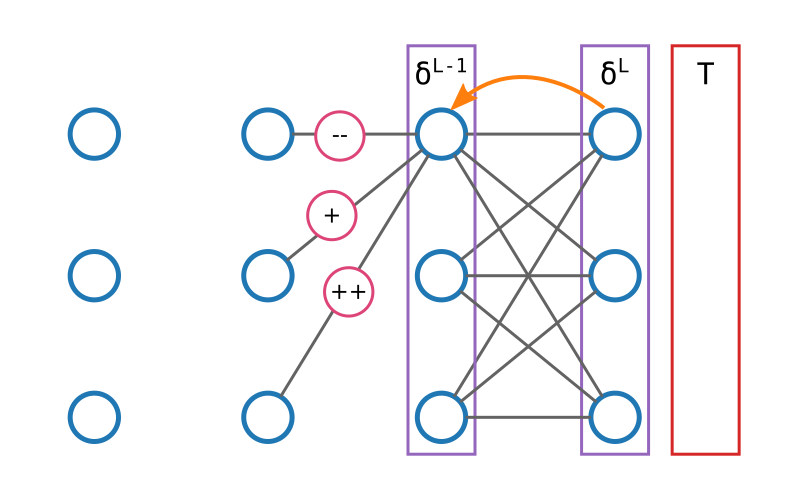
Et si nous connaissons l'erreur de l'avant-dernière couche, nous pouvons calculer l'erreur de la couche précédente, et ainsi de suite, jusqu'à la première.
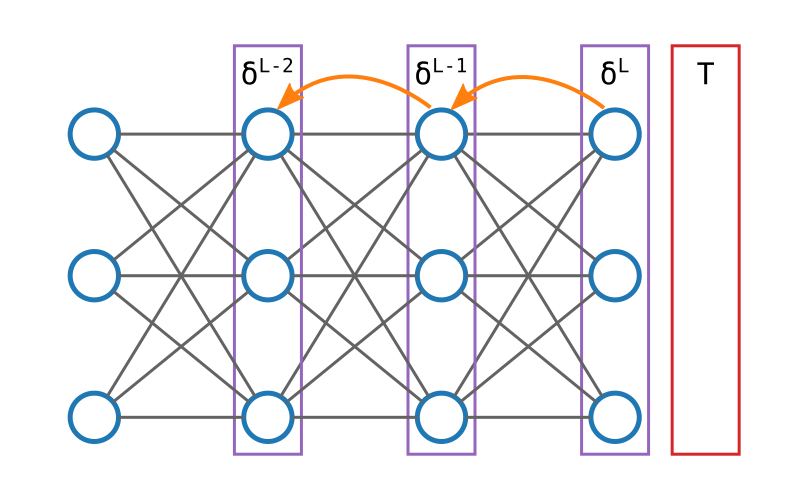
Une fois que nous avons obtenu l'erreur de toutes les couches, il nous est facile d'appliquer la même bête formule pour obtenir les dérivées partielles de tous les poids du réseau d'un seul coup.
Ainsi, en une seule passe vers l'avant suivie d'une seule passe vers l'arrière, nous avons potentiellement calculé des millions de dérivées partielles d'une manière algorithmiquement efficace. C'est cette propagation de l'erreur du réseau vers l'arrière qui a donné son nom à l'algo de la rétropropagation du gradient.
Voici le pseudo-code de l'algorithme d'apprentissage d'un réseau de neurones (algorithme du gradient + rétropropropagation du gradient) :
Initialiser le modèle avec les poids aléatoires
Tant que l'entraînement n'est pas terminé :
Pour chaque exemple de la liste des données d'entraînement :
Donner l'entrée au modèle pour obtenir la sortie
Calculer l'erreur en comparant la sortie avec le résultat attendu
Propager l'erreur de couche en couche vers l'arrière
Mettre à jour tous les poids du réseau
Il ne s'agissait ici que de décrire sommairement le fonctionnement de l'algorithme. Je sais que vous trépignez d'impatience à l'idée d'une étude plus approfondie bourrée d'équations interminables, je ne vous ferai pas languir plus longtemps.
Calculer l'erreur pour la dernière couche
Nous avons le pseudo-code de l'algorithme, mais il nous reste plusieurs éléments à expliquer plus en détails :
- comment calculer δL exactement ?
- comment propager l'erreur de couche en couche ?
- comment utiliser l'erreur pour calculer toutes les dérivées partielles ?
Pour répondre à ces questions, il nous faut étudier comment la modification d'un seul poids peut impacter le résultat de la fonction de coût.
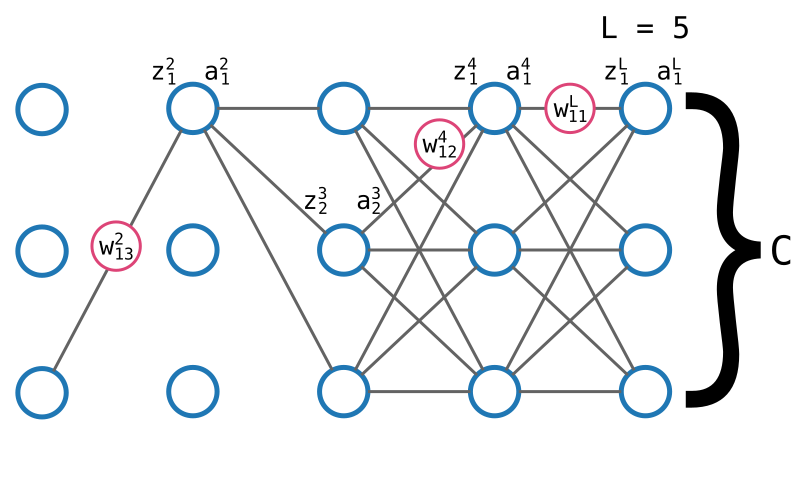
Imaginons que dans le réseau de neurones illustré ci-dessus, pris d'un coup de folie, je décide de modifier un tout petit peu le poids \(w^L_{11}\) en lui ajoutant une petite valeur que je noterai \(\Delta w^1_{11}\).
En modifiant ce poids, je modifie la valeur de sortie du réseau, en donc la valeur calculée par la fonction de coût. Cette modification de la valeur C, je la noterai \(\Delta C\).
Par définition, on a l'équation suivante :
$$ \frac{\partial C}{\partial w^L_{11}} \Delta w^L_{11} = \Delta C $$
Car, on le rappelle, \(\partial C / \partial w^L_{11}\) est la valeur qui mesure la variation de C en fonction de \(w^L_{11}\).
On peut mieux comprendre comment une variation de \(w^L_{11}\) impacte C en détaillant les impacts sur les valeurs intermédiaires.
D'abord, modifier \(w^L_{11}\) va modifier le calcul de \(z^L_1\). En suivant l'exemple ci-dessus, on peut modéliser cet impact de la façon suivante :
$$ \frac{\partial z^L_1}{\partial w^L_{11}} \Delta w^L_{11} = \Delta z^L_1 $$
Puisque \(z^L_1\) est utilisé pour calculer \(a^L_1\), il est évident qu'une variation du premier aura un impact sur le second.
$$ \frac{\partial a^L_1}{\partial z^L_1} \Delta z^L_1 = \Delta a^L_1 $$
Enfin, puisque la fonction de coût dépend de la sortie du réseau, une variation de \(a^L_1\) fait varier C.
$$ \frac{\partial C}{\partial a^L_1} \Delta a^L_1 = \Delta C $$
En considérant les trois équations précédentes, il est facile d'effectuer quelques remplacements et simplifications pour obtenir l'équation suivante :
$$ \frac{\partial C}{\partial w^L_{11}} = \frac{\partial z^L_1}{\partial w^L_{11}} \frac{\partial a^L_1}{\partial z^L_1} \frac{\partial C}{\partial a^L_1} $$
En clair : pour calculer comment w fait varier C, il suffit de calculer comment w fait varier z, comment z fait varier a, et comment a fait varier C. En fait, il ne s'agit ni plus ni moins que d'une illustration du théorème de dérivation des fonctions composées (chain rule en anglais).
En quoi cette nouvelle équation nous avance-t-elle ? Étudions ses termes séparément.
\(\partial C / \partial a^L_1\) est la variation de la fonction de coût en fonction de la sortie du réseau. Ce n'est rien d'autre que la dérivée de la fonction de coût.
$$ \frac{\partial C}{\partial a^L_1} = cost'(a^L_1) $$
Cette dérivée dépend évidemment de la fonction de coût utilisée, mais son calcul ne présente pas de problème particulier.
\(\partial a^L_1 / \partial z^L_1\) désigne la variation de la fonction d'activation en fonction de l'agrégation. Pour obtenir cette valeur, il nous suffit de calculer la dérivée de la fonction d'activation.
$$ \frac{\partial a^L_1}{\partial z^L_1} = \sigma'(z^L_1) $$
Enfin, \(\partial z^L_1 / w^L_{11}\) est la variation de la fonction d'agrégation en fonction de ce seul poids. En utilisant les règles usuelles de dérivation, il est possible de montrer que cette valeur est exactement égale à \(a^{L-1}_1\).
$$ \frac{\partial z^L_1}{\partial w^L_{11}} = a^{L-1}_1 $$
Si on récapitule, nous avons maintenant tout ce qu'il nous faut pour établir l'équation suivante :
$$ \frac{\partial C}{\partial w^L_{11}} = a^{L-1}_1 * \sigma'(z^L_1) * cost'(a^L_1) $$
Qu'on généralisera ainsi :
$$ \frac{\partial C}{\partial w^L_{ij}} = a^{L-1}_j * \sigma'(z^L_i) * cost'(a^L_i) $$
Dans un but d'optimisation, on calculera d'abord la valeur intermédiaire \(\delta^L_i = \sigma'(z^L_i) * cost'(a^L_i)\).
S'il vous reste un peu de matière grise en état de marche, vous n'aurez pas manqué de remarquer l'égalité suivante :
$$ \delta^L_i = \sigma'(z^L_i) * cost'(a^L_i) = \frac{\partial a^L_i}{\partial z^L_i} \frac{\partial C}{\partial a^L_i} = \frac{\partial C}{\partial z^L_i} $$
On obtient enfin :
$$ \frac{\partial C}{\partial w^L_{ij}} = a^{L-1}_j * \delta^L_i $$
On en remet une couche
Nous avons calculé l'erreur pour la dernière couche. Voyons maintenant comment nous pouvons remonter à la couche précédente.

Reprenons l'exercice précédent et étudions de quelle manière une modification du poids \(w^4_{12}\) (par exemple) fait varier C.
$$ \frac{\partial C}{\partial w^4_{12}} = \frac{\partial z^4_1}{\partial w^4_{12}} \frac{\partial a^4_1}{\partial z^4_1} \frac{\partial C}{\partial a^4_1} $$
Le premier terme \(\partial z^4_1 / w^4_{12}\) est la variation de la fonction d'agrégation en fonction de ce seul poids. En suivant le même raisonnement que tout à l'heure, on montre que cette valeur est exactement égale à \(a^{3}_2\).
Le second terme \(\partial a^4_1 / \partial z^4_1\) désigne toujours la variation de la fonction d'activation en fonction de l'agrégation. Nous avons déjà vu qu'il suffit de prendre la dérivée de la fonction Sigmoïde.
$$ \frac{\partial a^4_1}{\partial z^4_1} = \sigma'(z^4_1) $$
Enfin, il reste le dernier terme \(\partial C / \partial a^4_1\). Pour le calculer, nous utilisons encore la chaîne de dérivation. Il nous suffit de remarquer que si \(a^4_1\) est modifié, cela va avoir un impact sur les valeurs de \(z^L_1\), \(z^L_2\) et \(z^L_3\). On peut donc établir l'équation suivante :
$$ \frac{\partial C}{\partial a^4_1} = \frac{\partial z^L_1}{\partial a^4_1} \frac{\partial C}{\partial z^L_1} + \frac{\partial z^L_2}{\partial a^4_1} \frac{\partial C}{\partial z^L_2} + \frac{\partial z^L_3}{\partial a^4_1} \frac{\partial C}{\partial z^L_3} = \sum_{k} \frac{\partial z^L_k}{\partial a^4_1} \frac{\partial C}{\partial z^L_k} $$
(Prenez quelques secondes pour souffler, ça va passer.)
Et que voit-on apparaître sous nos yeux ébahis ?! Mais si ! là ! tout à droite… Nous retrouvons une vieille connaissance ! Ce dernier terme, nous l'avons déjà calculé !
$$ \frac{\partial C}{\partial z^L_k} = \delta^L_k $$
Il ne nous reste donc plus qu'à calculer \(\partial z^L_k / \partial a^4_1\), c'est à dire à calculer la variation des z de la couche suivante en fonction du a du neurone actuel. Honnêtement, si vous êtes arrivé·e jusque là, vous verrez que ce n'est pas très compliqué. Je vous laisse vérifier que :
$$ \frac{\partial z^L_k}{\partial a^4_1} = w^L_{k1} $$
Si nous récapitulons, nous avons donc :
$$ \frac{\partial C}{\partial w^4_{12}} = a^3_2 * \sigma'(z^4_1) * \sum_{k} w^L_{k1} \delta^L_k $$
Généralisation
Même si nous avons utilisé des poids spécifiques pour notre étude, nous avons assez d'éléments pour généraliser et écrire les équations nécessaire à l'implémentation de l'algorithme :
$$ \begin{array}{l} \delta^L_i = \sigma'(z^L_i) * cost'(a^L_i) \\ \\ \delta^l_i = \sigma'(z^l_i) * \sum_{j} w^{l+1}_{ji} \delta^{l+1}_{j} \\ \frac{\partial C}{\partial w^l_{ij}} = a^{l-1}_j \delta^l_i \\ \\ \frac{\partial C}{\partial b^l_{i}} = \delta^l_i \end{array} $$
Notez que la dernière équation est balancée en loucedé sans aucune justification. C'est parce que je suis en train de faire une indigestion de maths. Si vous voulez les détails, il faudra allez les chercher vous même.
Raffinement de gourmet
Nous avons toutes les formules nécessaires à l'implémentation. Nous allons néanmoins apporter un dernier raffinement à l'algorithme.
En effet, tel que décrit ici, nous mettons à jour les poids à chaque passe (une passe en avant, une passe en arrière, on met à jour les poids).
En pratique, on va plutôt utiliser la rétropropagation du gradient pour calculer les erreurs sur un certain nombre d'exemples, puis calculer la moyenne de ces erreurs, et seulement ensuite mettre à jour les poids. C'est un raffinement qui ne change pas fondamentalement le principe de l'algorithme, mais apporte un gain en efficacité et en rapidité.
Le code
Reprenons le code du billet précédent, avec
l'ajout de la fonction train.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.utils import shuffle
from sklearn.datasets import fetch_mldata
DATA_PATH = 'data'
def load_mnist_data():
"""Easy way to fetch and prepare mnist data."""
mnist = fetch_mldata('MNIST original', data_home=DATA_PATH)
# Dans MNIST, les données sont triées par labels (les 0 d'abord, les 1
# ensuite…), ce qui ne nous convient pas. Mélangeons-les.
X, y = shuffle(mnist.data, mnist.target)
# X est une matrice de taille(70000, 784)
# X[0] est la première image de la liste
# X[0][0] est le premier pixel de cette image
# y est une matrice de taille (70000,)
# y[0] est la valeur représentée par l'image X[0]
# Comme les valeurs des pixels sont exprimées entre 0 et 255, nous divisons
# par 255 pour obtenir des valeurs comprises entre 0 et 1.
return X / 255.0, y
def sigmoid(x):
return 1.0 / (1.0 + np.exp(-x))
def sigmoid_prime(x):
"""Dérivée de la fonction sigmoid."""
return sigmoid(x) * (1.0 - sigmoid(x))
def to_one_hot(y, k):
"""Convertit un entier en vecteur "one-hot".
to_one_hot(5, 10) -> (0, 0, 0, 0, 1, 0, 0, 0, 0)
"""
one_hot = np.zeros(k)
one_hot[y] = 1
return one_hot
class Layer:
"""Une seule couche de neurones."""
def __init__(self, size, input_size):
self.size = size
self.input_size = input_size
# Les poids sont représentés par une matrice de n lignes
# et m colonnes. n = le nombre de neurones, m = le nombre de
# neurones dans la couche précédente.
self.weights = np.random.randn(size, input_size)
# Un biais par neurone
self.biases = np.random.randn(size)
# Résultat du calcul de chaque neurone.
# Il est important de noter que `data` est un vecteur (normalement, de
# longueur `self.input_size`, et que nous retournons un vecteur de
# taille `self.size`.
def forward(self, data):
aggregation = self.aggregation(data)
activation = self.activation(aggregation)
return activation
# Calcule la somme des entrées pondérées + biais pour chaque neurone.
# Plutôt que d'utiliser une boucle for, nous tirons parti du calcul
# matriciel qui permet d'effectuer toutes ces opérations d'un coup.
def aggregation(self, data):
return np.dot(self.weights, data) + self.biases
# Passe les valeurs aggrégées dans la moulinette de la fonction
# d'activation.
# `x` est un vecteur de longueur `self.size`, et nous retournons un
# vecteur de même dimension.
def activation(self, x):
return sigmoid(x)
# Dérivée de la fonction d'activation.
def activation_prime(self, x):
return sigmoid_prime(x)
# Mise à jour des poids à partir du gradient (algo du gradient)
def update_weights(self, gradient, learning_rate):
self.weights -= learning_rate * gradient
# Idem mais avec les biais
def update_biases(self, gradient, learning_rate):
self.biases -= learning_rate * gradient
class Network:
"""Un réseau constitué de couches de neurones."""
def __init__(self, input_dim):
self.input_dim = input_dim
self.layers = []
def add_layer(self, size):
if len(self.layers) > 0:
input_dim = self.layers[-1].size
else:
input_dim = self.input_dim
self.layers.append(Layer(size, input_dim))
# Propage les données d'entrée d'une couche à l'autre.
def feedforward(self, input_data):
activation = input_data
for layer in self.layers:
activation = layer.forward(activation)
return activation
# Retourne l'index du neurone de sortie qui a la plus haute valeur, ce
# qui revient à indiquer quelle classe est sélectionnée par le réseau.
def predict(self, input_data):
return np.argmax(self.feedforward(input_data))
# Évalue la performance du réseau à partir d'un set d'exemples.
# Retourne un nombre entre 0 et 1.
def evaluate(self, X, Y):
results = [1 if self.predict(x) == y else 0 for (x, y) in zip(X, Y)]
accuracy = sum(results) / len(results)
return accuracy
# Fonction d'entraînement du modèle.
# Comme décrit dans le billet, nous allons faire tourner la
# rétropropagation sur un certain nombre d'exemples (batch_size) avant
# de calculer un gradient moyen, et de mettre à jour les poids.
def train(self, X, Y, steps=30, learning_rate=0.3, batch_size=10):
n = Y.size
for i in range(steps):
# Mélangeons les données parce que… parce que.
X, Y = shuffle(X, Y)
for batch_start in range(0, n, batch_size):
X_batch, Y_batch = X[batch_start:batch_start + batch_size], Y[batch_start:batch_start + batch_size]
self.train_batch(X_batch, Y_batch, learning_rate)
# Cette fonction combine les algos du retropropagation du gradient +
# gradient descendant.
def train_batch(self, X, Y, learning_rate):
# Initialise les gradients pour les poids et les biais.
weight_gradient = [np.zeros(layer.weights.shape) for layer in self.layers]
bias_gradient = [np.zeros(layer.biases.shape) for layer in self.layers]
# On fait tourner l'algo de rétropropagation pour calculer les
# gradients un certain nombre de fois. On fera la moyenne ensuite.
for (x, y) in zip(X, Y):
new_weight_gradient, new_bias_gradient = self.backprop(x, y)
weight_gradient = [wg + nwg for wg, nwg in zip(weight_gradient, new_weight_gradient)]
bias_gradient = [bg + nbg for bg, nbg in zip(bias_gradient, new_bias_gradient)]
# C'est ici qu'on calcule les moyennes des gradients calculés
avg_weight_gradient = [wg / Y.size for wg in weight_gradient]
avg_bias_gradient = [bg / Y.size for bg in bias_gradient]
# Il ne reste plus qu'à mettre à jour les poids et biais en
# utilisant l'algo du gradient descendant.
for layer, weight_gradient, bias_gradient in zip(self.layers,
avg_weight_gradient,
avg_bias_gradient):
layer.update_weights(weight_gradient, learning_rate)
layer.update_biases(bias_gradient, learning_rate)
# L'algorithme de rétropropagation du gradient.
# C'est là que tout le boulot se fait.
def backprop(self, x, y):
# On va effectuer une passe vers l'avant, une passe vers l'arrière
# On profite de la passe vers l'avant pour stocker les calculs
# intermédiaires, qui seront réutilisés par la suite.
aggregations = []
activation = x
activations = [activation]
# Propagation pour obtenir la sortie
for layer in self.layers:
aggregation = layer.aggregation(activation)
aggregations.append(aggregation)
activation = layer.activation(aggregation)
activations.append(activation)
# Calculons la valeur delta (δ) pour la dernière couche
# en appliquant les équations détaillées plus haut.
target = to_one_hot(int(y), 10)
delta = self.get_output_delta(aggregation, activation, target)
deltas = [delta]
# Phase de rétropropagation pour calculer les deltas de chaque
# couche
# On utilise une implémentation vectorielle des équations.
nb_layers = len(self.layers)
for l in reversed(range(nb_layers - 1)):
layer = self.layers[l]
next_layer = self.layers[l + 1]
activation_prime = layer.activation_prime(aggregations[l])
delta = activation_prime * np.dot(next_layer.weights.transpose(), delta)
deltas.append(delta)
# Nous sommes parti de l'avant-dernière couche pour remonter vers
# la première. deltas[0] contient le delta de la dernière couche.
# Nous l'inversons pour faciliter la gestion des indices plus tard.
deltas = list(reversed(deltas))
# On utilise maintenant les deltas pour calculer les gradients.
weight_gradient = []
bias_gradient = []
for l in range(len(self.layers)):
# Notez que l'indice des activations est « décalé », puisque
# activation[0] contient l'entrée (x), et pas l'activation de
# la première couche.
prev_activation = activations[l]
weight_gradient.append(np.outer(deltas[l], prev_activation))
bias_gradient.append(deltas[l])
return weight_gradient, bias_gradient
# Calcule le delta pour la dernière couche, en utilisant
# les dernières valeurs d'aggregation, d'activation, et la valeur
# cible.
# Notez que lorsque l'on utilise l'entropie croisée pour fonction de
# coût, l'équation de calcul de delta peut-être simplifiée pour aboutir
# au résultat ci dessous.
# Cf http://neuralnetworksanddeeplearning.com/chap3.html#the_cross-entropy_cost_function
def get_output_delta(self, z, a, target):
return a - target
if __name__ == '__main__':
# Découpons notre base de données en deux.
# Une partie pour l'entraînement du réseau, l'autre pour vérifier
# sa performance.
X, Y = load_mnist_data()
X_train, Y_train = X[:60000], Y[:60000]
X_test, Y_test = X[60000:], Y[60000:]
net = Network(input_dim=784)
net.add_layer(200)
net.add_layer(10)
accuracy = net.evaluate(X_test, Y_test)
print('Performance initiale : {:.2f}%'.format(accuracy * 100.0))
for i in range(30):
net.train(X_train, Y_train, steps=1, learning_rate=3.0)
accuracy = net.evaluate(X_test, Y_test)
print('Nouvelle performance : {:.2f}%'.format(accuracy * 100.0))
Je vous laisse lire le code en détail pour bien vous imprégner du truc. J'ai un peu joué avec différentes structures de graphe (nombre de couches, taille de chaque couche, etc.), jusqu'à obtenir un résultat à peu près sympathique.
Vous pouvez lancer le code ainsi :
python mnist2.py
Ensuite, levez-vous, pratiquez quelques étirements, refaites du café, sortez le chien, promenez les poubelles, relisez le best-of de Dostoïevski, n'oubliez pas de braquer un ventilateur vers votre processeur et armez vous de patience, parce que le machin risque de prendre un bout de temps.
Néanmoins, votre patience sera récompensée :
Performance initiale : 10.66%
Nouvelle performance : 92.78%
Nouvelle performance : 94.14%
Nouvelle performance : 95.13%
…
Célébration
Le modèle utilisé reste beaucoup trop simple, et le code est de toute manière sous-optimisé. Mais qu'importe ! Nous avons construit un algorithme capable de reconnaître l'écriture humaine avec une précision supérieure à 95% ! Même si on est loin de l'état de l'art, c'est un résultat suffisamment significatif pour qu'il mérite d'être célébré (comment ça, « toutes les occasions sont bonnes pour picoler ? »).
Pour aller plus loin
Ceci conclut notre étude de l'algorithme de la rétropropagation du gradient, et notre introduction aux principes du deep-learning.
Nous n'avons pourtant fait qu'effleurer les concepts et technologies du deep-learning, et il reste bien des choses à voir. Voici quelques exemples.
Nous n'avons pas abordé la problématique du surapprentissage (quand le modèle fonctionne correctement sur les données d'apprentissage, mais obtient de mauvais résultats sur de nouvelles données), et les techniques pour l'éviter.
Nous n'avons étudié qu'un seul type de modèle : les réseaux de neurones pleinement connectés (chaque couche est complètement connecté à la suivante). Il existe d'autres types de modèles, comme les réseaux récurrents, qui permettent de prendre en compte une dimension séquentielle dans les données, ou les réseaux convolutifs, particulièrement adaptés aux traitements d'images.
Nous n'avons pas parlé des nombreux raffinements de l'algo du gradient qui permettent un apprentissage plus efficace.
Bref ! Il reste du boulot. Mais ça sera pour la prochaine fois.