Au commencement était le vide. Puis vint… le neurone ! Et avec le neurone, l'explosion de l'intelligence, l'apparition et la chute de civilisations toutes plus complexes les unes que les autres, jusqu'à l'émergence de notre monde, une société moderne, aboutie, ou interagissent en permanence des millions d'êtres vivants forgés dans les flammes multimillénaires de l'évolution. Grâce à sa précieuse matière grise, réceptacle miraculeux de milliards de milliards de neurones, chaque humain est doué d'une capacité cérébrale prodigieuse, capable de prouesses mentales incomparables dans l'univers connu, apte à jongler avec des concepts théoriques et abstraits pour concevoir, planifier, explorer, découvrir, créer, démasquer en un clin d'œil les justifications vaseuses des politiciens véreux détournant des millions d'argent public… Ah, non, autant pour moi. Oubliez tout ce que j'ai dit à propos d'« explosion de l'intelligence ».

Bref…

Après une introduction au machine learning, nous avions implémenté un premier algorithme pour aborder les concepts utiles, tels que la modélisation de problème, la notion de fonction de coût et d'algorithme d'apprentissage. Nous avions ensuite étudié un cas un poil plus complexe, qui nous a permis d'aborder la régression logistique, la fonction sigmoïde, le feature scaling, de réviser les notions de dérivées partielles et d'entraîner un modèle à plusieurs paramètres.

Il faut bien le reconnaître, les exemples étudiés jusqu'à maintenant étaient d'une utilité toute relative. Hors, si l'on fait aujourd'hui tout un foin du machine learning, c'est que les technologies qui en découlent permettent de réaliser des choses autrement plus impressionnantes.

Aujourd'hui, je vous propose d'utiliser les connaissances acquises pour aller plus loin et aborder véritablement le deep learning.

Deep learning, watizit ?

Dans un précédent billet, j'ai qualifié le deep learning de buzzword, c'est une grossière exagération. Le machine learning est un domaine très vaste, le deep learning n'en est qu'une branche, mais qui offre néanmoins un champ d'étude étendu.

Le deep learning est très à la mode ; comme pour la blockchain ou le no-sql en son temps, on l'applique à tous bouts de champ sans discernement, parfois plus pour séduire des investisseurs ou se faire plaisir que par réelle utilité.

Quelles sont les spécificités du deep learning, et quelles en sont les utilisations pertinentes ?

S'il te plaît… modélise-moi des données

Nous avons vu que le machine learning consiste en l'utilisation d'algorithmes (dits « d'apprentissage ») pour bâtir de manière plus ou moins automatique des modèles de données. On rappelle que « modèle de données » signifie une « traduction des données dans une forme — n'importe laquelle on s'en fout — utilisable, par exemple une grosse équation ou une bête fonction python ou javascript ».

Par exemple, en récupérant des captures d'écrans d'annonces immobilières sur le Bon Coin, j'obtiens des données brutes inutilisables. Si je m'intéresse au prix de l'immobilier, un modèle pertinent pourrait être une fonction qui prendrait comme paramètres un certain nombre de critères numériques (surface, nombre de pièces, etc.) et qui retournerait un nombre entier se rapprochant le plus possible du prix de vente effectivement constaté.

Un modèle peut être plus ou moins complexe. En l'occurrence, une des spécificités du deep learning est que cela permet de modéliser des données avec un haut niveau d'abstraction. Niveau d'abstraction ? Mais encore ?

Considérons une image : d'un point de vue informatique, il ne s'agit que d'une liste de pixels, c'est à dire de nombres entiers. Un modèle avec un faible niveau d'abstraction va construire une représentation très proche de la donnée brute : il n'ira pas plus loin que le pixel et convertira les données brutes en points colorés. Un tel modèle peut être utile si mon seul but est d'afficher l'image ou de la redimensionner, par exemple.

Avec un niveau d'abstraction un peu plus élevé, un modèle pourra commencer à extraire des informations plus abstraites, de plus haut niveau. Par exemple, on travaillera au niveau des contrastes, des formes, des zones de couleurs… Un tel modèle permettrait de régler les problèmes d'exposition, rendre les couleurs plus vibrantes, etc.

En augmentant encore le niveau d'abstraction, on pourra par exemple reconnaître des objets dans l'image : présence d'un chaton, d'un ballon ou d'une voiture, d'un ancien premier ministre en train de détourner des fonds, etc.

On pourrait imaginer des niveaux d'abstractions encore plus élevés, permettant d'extraire un style artistique, ou de déterminer que l'image représente un événement joyeux, suscite telle émotion ou illustre métaphoriquement telle idée.

On peut réaliser le même exercice pour des données textuelles. Niveau d'abstraction faible : le caractère. Plus élevé : les mots. Encore plus élevé : les paragraphes. Encore plus élevé : les concepts, les idées, la thèse, etc.

La killer feature du deep learning, c'est qu'on peut insérer les données brutes (pixels) d'un côté, indiquer le niveau d'abstraction qui nous intéresse à la sortie (un chat), et laisser le modèle déterminer automatiquement les abstractions intermédiaires dont il aura besoin, de la même manière qu'un humain combinera des concepts simples pour former des pensées complexes.

Vous comprenez maintenant que le deep-learning consiste à modéliser des données avec un niveau élevé d'abstraction. Tout ceci est bel et bon, mais à quoi cela sert-il ?

Les utilisations du deep learning

Avec un programme capable de manipuler des pixels, vous pouvez effectuer des traitements basiques sur une image : l'éclaircir ou l'assombrir, changer des couleurs, etc. Si votre programme est capable de gérer des formes, des contrastes, vous pouvez effectuer des actions plus complexes et intéressantes : régler les problèmes d'exposition, donner plus de punch à l'image, etc. Imaginez maintenant un programme capable de jongler avec des concepts beaucoup plus abstraits. Que pourriez-vous faire ?

Il s'avère que la réponse est « des trucs de ouf ! ». Par exemple, vous pouvez transformer un croquis rapide en dessin bien propre. Ou coloriser automatiquement des images en noir et blance. Ou convertir la photo du premier péquenaud venu en modèle 3d en un clin d'œil. Ou créer des visages à partir de croquis. Ou faire réciter des blagues de Toto à Vladimir Poutine. Ou synthétiser des images à partir de texte. Ou transformer n'importe quel gribouillis en œuvre d'art. Ou géolocaliser automagiquement n'importe quelle photo.

Un seul de ces exemples aurait suffit à me faire pendouiller la mâchoire, et je pourrais en trouver encore des dizaines d'autres. Et l'on a parlé que d'images. Imaginez la même chose avec les sons, les vidéos, ou d'autres types de données plus complexes.

Le deep learning ne désigne pas une technique particulière mais une série d'outils qui peuvent être combinés et recombinés, un peu comme un langage de programmation de très haut niveau. C'est ce qui explique la versatilité de ces technologies.

Deeper et sans reproches

Nous savons à quoi sert le deep learning. Comment cela fonctionne-t-il ?

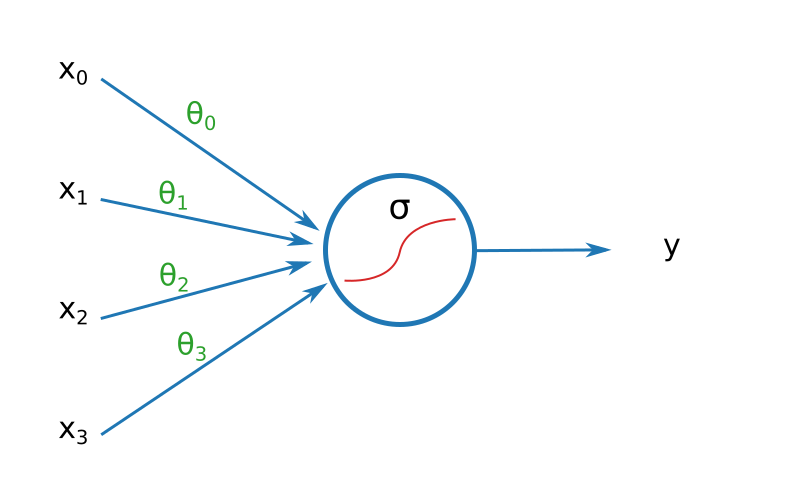
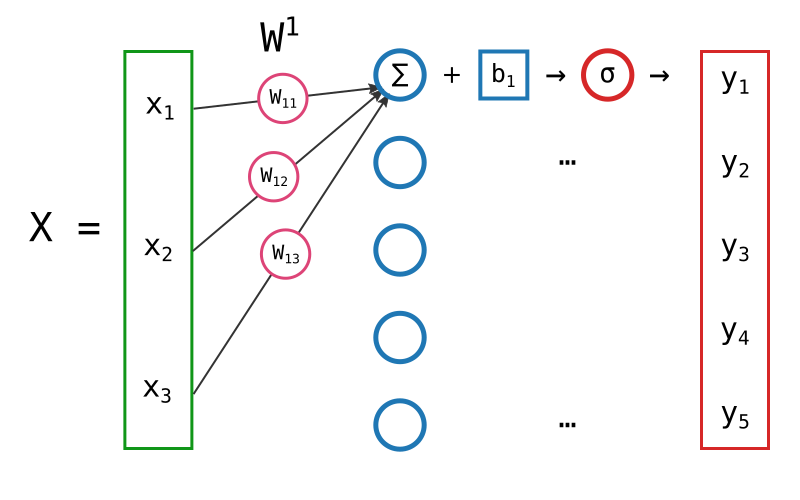
Dans le billet précédent, nous avions utilisé un modèle très simple : une bête fonction faisant la somme des entrées pondérées avant de passer le tout dans la moulinette de la fonction Sigmoïde.

Il s'avère que ce modèle ressemble très fort à la brique de base utilisée en deep learning : le neurone.

On parle de neurone parce que si fouilliez dans vos cartons pour retrouver de vieux manuels de SVT et les ouvrir au chapitre « fonctionnement du cerveau », vous remarqueriez que le schéma ci-dessus ressemble vaguement à un véritable neurone, avec ses dendrites, ses axones et tout le tralala. D'aucuns suggèrent que le fonctionnement des modèles à base de neurones n'est pas sans rappeler celui de notre propre cerveau. Honnêtement, l'analogie n'est d'aucune aide pour comprendre le deep learning, aussi la laisserons nous de côté. Le terme de « neurone » est resté, et nous sommes bien obligés de le conserver. Dorénavant, quand j'utiliserai le terme de neurone, je parlerai du truc dessiné plus haut, pas des machins que vous avez (peut-être si vous avez de la chance) dans votre cerveau.

Pour bien comprendre un neurone, on peut l'imaginer comme une petite unité décisionnelle, c'est à dire un « machin » qui récupère des données, les évalue pour prendre une décision, et crache la réponse.

« Est-ce qu'on sort ce soir ? » Prendre cette décision nécessite de considérer un certain nombre de paramètres. Est-ce qu'il pleut ? Est-ce qu'il y a un super film à la télé ? Est-ce que nos ami·e·s boute-en-train sont en ville ?

$$ X = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} \text{intensité de la pluie} \\ \text{mon envie de voir le film qui passe ce soir} \\ \text{funitude des ami-e-s que nous sommes censés retrouver} \end{pmatrix} $$

Mon envie de sortir ce soir dépendra de l'importance que j'accorde à ces différents paramètres. Peut-être qu'une grosse pluie me donnera envie de rester à la maison, mais pas tant que ça parce que j'ai passé toute ma jeunesse en Normandie, alors que je serai très motivé si je sais que mes potes sont en ville.

À ces différents poids, il faut ajouter un élément : le biais. À données et poids égaux, un neurone donné sera plus ou moins biaisé en fonction de telle ou telle décision. Par exemple, mon neurone « on sort ce soir » est plutôt biaisé en direction d'une réponse négative (parce que je suis un fainéant asocial), tandis que celui de ma femme, qui est une personne normalement constituée, est plutôt biaisé en direction d'une réponse positive.

Prendre une décision nécessitera de considérer tous ces paramètres avant de les passer dans une fonction d'activation : c'est la fameuse moulinette qui transforme une valeur arbitraire en une valeur utilisable. La fonction d'activation est arbitraire, et ce sera de toutes façons à nous d'interpréter la sortie du neurone. En revanche, il faut que la fonction utilisée réponde à certains critères dont l'évocation nous emmènerait trop loin. Nous avons pour le moment utilisé la fonction Sigmoïde, et nous continuerons sur notre lancée.

Si l'on devait implémenter un seul neurone en Python, voici à quoi pourrait ressembler le code :

import numpy as np

def sigmoid(x):
    return 1.0 / (1.0 + np.exp(-x))

class Neuron:
    def __init__(self, input_size):
        """Initialisation des poids / biais avec des valeurs aléatoires."""
        self.weights = np.random.randn(input_size)
        self.bias = np.random.randn()

    def activation(self, X):
        """On suppose que X est de la taille passée dans le constructeur."""
        aggregation = np.sum(X * self.weights) + self.bias
        return sigmoid(aggregation)

En rajouter une couche

La classe politique française ne manque pas de personnalités démontrant avec brio qu'avec un seul neurone, on ne peut se faire du monde qu'une idée relativement dénuée de subtilité.

Pour réaliser des modèles plus complexes, et donc plus puissants, il faudra combiner entre eux un gros paquet de neurones. Et pas n'importe comment : en couches.

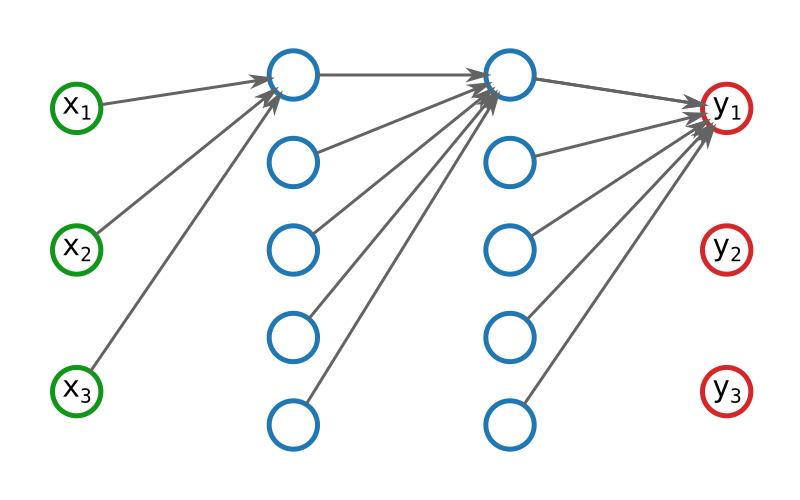
Ce type de modèle, constitué de neurones mis en réseau, s'appelle un… réseau de neurones. Super original ! Les scientifiques, un peu de poésie, ça vous étoufferait ? Bref… Dans un tel réseau, les données sont balancées dans la première couche, la couche d'entrée. Chaque neurone fait sont petit calcul avant de cracher sa réponse, qui sera récupérée par les neurones de la couche suivante, etc. et ce jusqu'à la dernière couche : la couche de sortie.

Fait amusant : il existe une astuce pour repérer les nouveaux parents. Ce sont ceux qui tressaillent quand on parle de remplir la couche de sortie (désolé, il fallait que j'en fasse au moins une).

Traditionnellement, la première couche est représentée comme les autres, alors qu'il ne s'agit pas de neurones, ce sont simplement les données d'entrée.

Deux couches successives ne contiennent pas forcément le même nombre de neurones. En règle général, plus un modèle est profond (plus de couches), plus il sera capable d'apprendre des concepts abstraits, mais plus il sera difficile de les lui faire apprendre.

Lorsque nous avons travaillé avec un seul neurone, nous avions un modèle avec n + 1 paramètres, n étant la taille de la donnée d'entrée. Vous constaterez facilement que le nombre de paramètres de notre modèle vient d'exploser. Reprenons l'exemple du réseau ci-dessus : chaque arrête de neurone à neurone est pondérée, et chaque neurone utilise un biais.

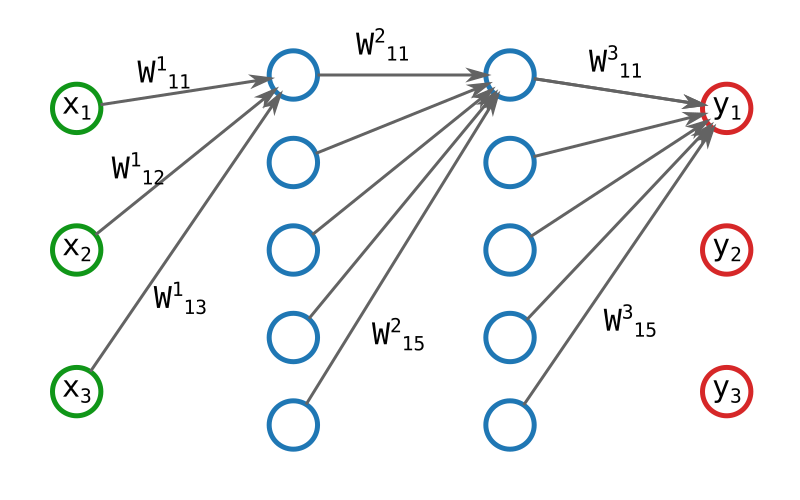
Le calcul du nombre exact de paramètres du modèle est laissé à l'internaute.

Exemple de réseau de neurones

Comment un tel réseau peut-il nous aider ? En quoi ce type de modèle peut-il fournir des fonctionnalités quasi-magiques comme celles mentionnées plus haut ? Voyons ceci avec un exemple.

Il est un jeu de données très utilisé dans le monde du machine learning : c'est la base MNIST. Il s'agit d'une « petite » source de données qui consiste en 70000 images en noir et blanc de 28x28 pixels représentant des chiffres écrits à la main. À chaque image correspond un label, c'est à dire le chiffre représenté.

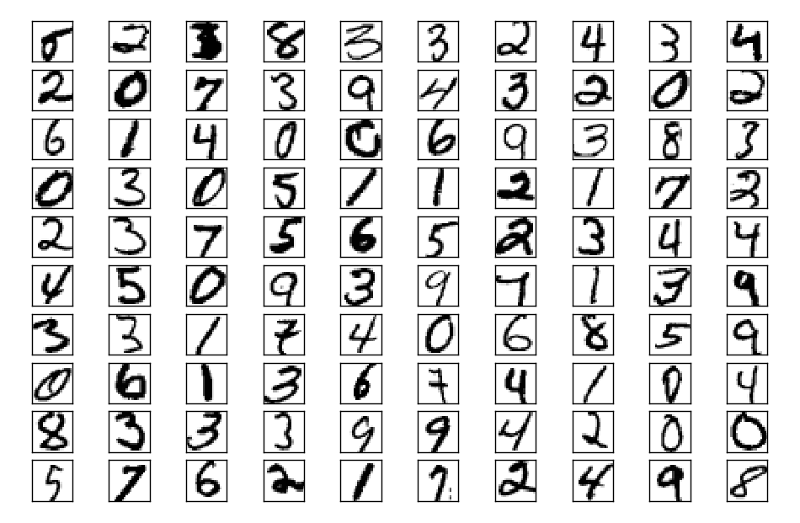
MNIST est le jeu de données consacré pour les tutoriels sur le machine learning et les problèmes de reconnaissance d'image, et il ne sera pas dit que j'ai failli à la tradition.

Si nous devions coder à la main un programme capable d'analyser une image pour déterminer le chiffre représenté, comment procéderions nous ?

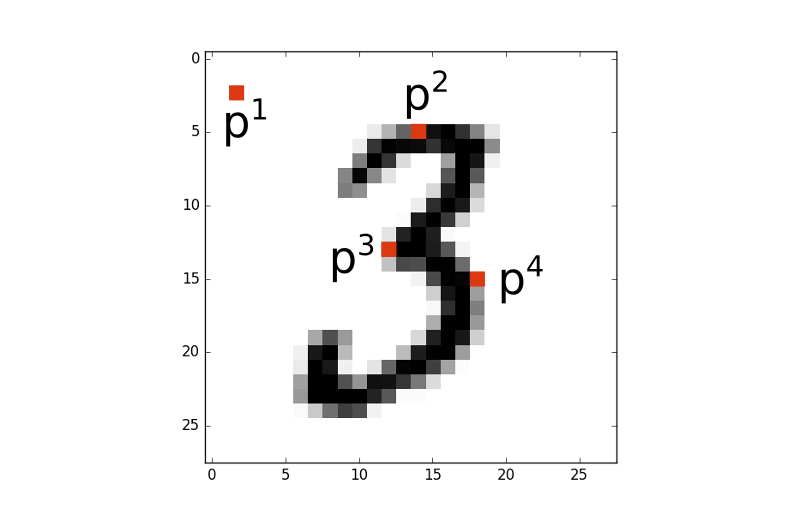
Intuitivement, lorsque je regarde ce type d'image, une première solution me vient à l'esprit. J'ai envie de considérer chaque pixel un par un et de vérifier s'il fait plutôt pencher la balance vers une solution ou l'autre.

Considérez l'image ci-dessus. Le pixel p⁴ sera souvent allumé si le chiffre est un 3, un 5, un 6, un 8 ou un 0. En revanche, il le sera rarement si le chiffre est un 1. Par conséquent, je peux écrire dans mon code quelque chose comme ça :

si p4:
    score[3]++
    score[5]++
    …
    score[1]--

Si le pixel p³ est allumé, il est très probable que l'image ne représente pas un 0.

si p3:
    score[0]--

En revanche, le pixel p¹ ne sera pratiquement jamais allumé (le pauvre), et sa valeur ne m'indique pas grand chose.

si p1:
    pass

Ainsi de suite. Après avoir traité tous les pixels, il me suffit de retourner le chiffre qui a obtenu le score le plus élevé.

return score.indexOf(score.max())

Si je sélectionne correctement le poids que j'affecte à chaque pixel, cette solution, bien que fastidieuse, peut n'être pas trop mauvaise.

Néanmoins, toujours intuitivement, cette solution reste sous-optimale. En effet, peut-être qu'un pixel donné sera plutôt indicateur d'un chiffre ou d'un autre en fonction de la valeur d'autres pixels. Ce qu'il faudrait, c'est introduire un niveau de profondeur supplémentaire pour augmenter le niveau d'abstraction de la fonction.

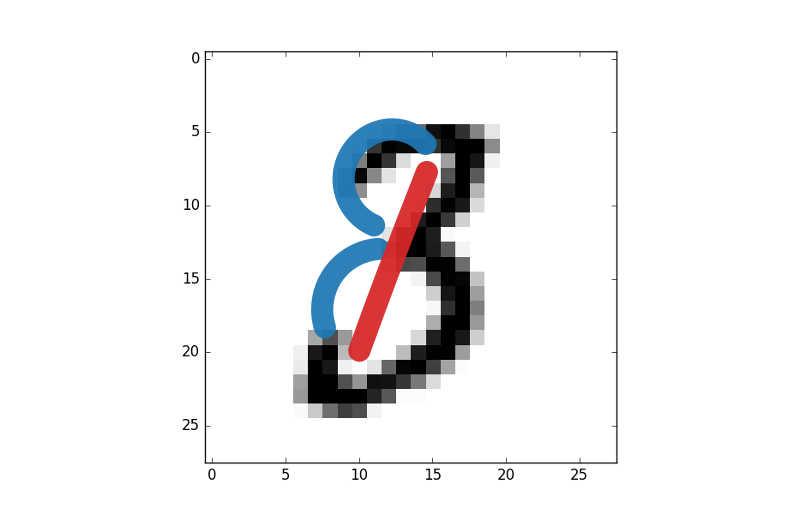
S'il y a une barre verticale au milieu de l'image, il s'agit peut-être d'un 1, d'un 4, d'un 7 ou d'un 9, mais s'il y a en plus une boucle en haut à gauche, alors il s'agit presque certainement d'un 9.

S'il y a une boucle en haut à gauche, il s'agit peut-être d'un 3, d'un 8 ou d'un 9, mais s'il y a aussi une boucle en bas à gauche, alors il s'agit très certainement d'un 8.

D'une manière assez grossière, c'est de cette manière que fonctionne un réseau de neurone. En utilisant une seule couche, vous comme si vous considériez l'image pixel par pixel. En ajoutant une seconde couche, vous donnez au modèle l'opportunité de construire une abstraction plus élevée, et donc d'obtenir de meilleurs résultats.

Comment dimensionner son réseau neuronal ?

Dans le cadre de la mise en place d'un modèle à base de réseau neuronal, la couche d'entrée est généralement dictée par les données. Ici, chaque image fait 28x28 pixels, donc un tableau de 784 valeurs. Nous aurons donc une première couche de 784 neurones.

La couche de sortie dépend du résultat attendu. Nous voulons savoir à quel chiffre correspond l'image, une idée relativement intuitive consisterait à utiliser un seul neurone qui renverrait un chiffre entre 0 et 9. Toutefois, ce type de solution fonctionne en pratique assez mal, et l'on a plutôt tendance à utiliser un neurone par possibilité dans l'éventail des solutions. Notre couche de sortie sera donc composée de 10 neurones.

Et au milieu ? Et bien, c'est freestyle. Il existe évidemment des heuristiques, mais il n'y a pas (encore ?) de méthode systématique pour dimensionner un réseau de neurones de manière optimale.

À la question : « combien de couches », la réponse est « le moins possible pour néanmoins obtenir des résultats pertinents ». On pourra par exemple commencer avec une seule couche, et tester la pertinence du modèle.

À la question : « combien de neurones par couches », on pourra par exemple commencer par un nombre intermédiaire entre la couche d'entrée et la couche de sortie.

À vrai dire, à ces deux questions, la bonne réponse sera généralement « ça dépend ». L'expérience et les tests permettront de s'approcher de la bonne architecture.

Implémenter une solution au MNIST en Python

Du code, bordel !

S'il est possible d'implémenter un réseau de neurones en js, il reste tout de même redoutablement plus efficace (et moins frustrant) d'utiliser un langage proposant de véritables librairies de calcul scientifique. Nous nous tournerons donc vers Python. Tout le code qui va suivre est à entasser dans le même fichier.

Notez qu'il existe de très bons outils hautement optimisés pour le deep learning, le code suivant n'a aucun intérêt sinon pédagogique.

En guise de dépendance, nous utiliserons la librairie numpy pour ses primitives d'algèbre linéaire. Nous installerons aussi scikit-learn pour son helper qui permet de récupérer la base MNIST sans nous casser la tête.

pip install numpy scikit-learn

Voici les imports utilisés :

import numpy as np
from sklearn.utils import shuffle
from sklearn.datasets import fetch_mldata

Commençons par écrire une petite fonction d'aide destinée à charger les données d'entraînement / test en mémoire.

DATA_PATH = 'data'


def load_mnist_data():
    """Télécharge et prépare la base MNIST"""

    # télécharge dans le sous répertoire local ./data/
    mnist = fetch_mldata('MNIST original', data_home=DATA_PATH)

    # Dans MNIST, les données sont triées par labels (les 0 d'abord, les 1
    # ensuite…), ce qui ne nous convient pas. Mélangeons-les.
    X, y = shuffle(mnist.data, mnist.target)

    # X est une matrice de taille(70000, 784)
    # X[0] est la première image de la liste
    # X[0][0] est le premier pixel de cette image
    # y est une matrice de taille (70000,)
    # y[0] est la valeur représentée par l'image X[0]

    # Comme les valeurs des pixels sont exprimées entre 0 et 255, nous divisons
    # par 255 pour obtenir des valeurs comprises entre 0 et 1.
    return X / 255.0, y

Nous allons construire le code minimal pour obtenir un réseau de neurone en état de fonctionner. Les poids et biais seront initialisés à des valeurs aléatoires, nous verrons plus loin comment fonctionne l'apprentissage.

Nous définissons également une fonction d'évaluation, qui vérifie le pourcentage de prédictions correctement réalisées par le réseau. Dans la mesure ou ces prédiction sont pour le moment aléatoires, nous devrions obtenir une valeur aux alentours de 10%.

# La fonction d'activation utilisée par le réseau
def sigmoid(x):
    return 1.0 / (1.0 + np.exp(-x))


class Layer:
    """Une seule couche de neurones."""
    def __init__(self, size, input_size):
        self.size = size
        self.input_size = input_size

        # Les poids sont représentés par une matrice de n lignes
        # et m colonnes. n = le nombre de neurones, m = le nombre de
        # neurones dans la couche précédente.
        self.weights = np.random.randn(size, input_size)

        # Un biais par neurone
        self.biases = np.random.randn(size)

    # Résultat du calcul de chaque neurone.
    # Il est important de noter que `data` est un vecteur (normalement, de
    # longueur `self.input_size`, et que nous retournons un vecteur de
    # taille `self.size`.
    def forward(self, data):
        aggregation = self.aggregation(data)
        activation = self.activation(aggregation)
        return activation

    # Calcule la somme des entrées pondérées + biais pour chaque neurone.
    # Plutôt que d'utiliser une boucle for, nous tirons parti du calcul
    # matriciel qui permet d'effectuer toutes ces opérations d'un coup.
    def aggregation(self, data):
        return np.dot(self.weights, data) + self.biases

    # Passe les valeurs aggrégées dans la moulinette de la fonction
    # d'activation.
    # `x` est un vecteur de longueur `self.size`, et nous retournons un
    # vecteur de même dimension.
    def activation(self, x):
        return sigmoid(x)


class Network:
    """Un réseau constitué de couches de neurones."""
    def __init__(self, input_dim):
        self.input_dim = input_dim
        self.layers = []

    def add_layer(self, size):
        if len(self.layers) > 0:
            input_dim = self.layers[-1].size
        else:
            input_dim = self.input_dim

        self.layers.append(Layer(size, input_dim))

    # Propage les données d'entrée d'une couche à l'autre.
    def feedforward(self, input_data):
        activation = input_data
        for layer in self.layers:
            activation = layer.forward(activation)
        return activation

    # Retourne l'index du neurone de sortie qui a la plus haute valeur, ce
    # qui revient à indiquer quelle classe est sélectionnée par le réseau.
    def predict(self, input_data):
        return np.argmax(self.feedforward(input_data))

    # Évalue la performance du réseau à partir d'un set d'exemples.
    # Retourne un nombre entre 0 et 1.
    def evaluate(self, X, Y):
        results = [1 if self.predict(x) == y else 0 for (x, y) in zip(X, Y)]
        accuracy = sum(results) / len(results)
        return accuracy


if __name__ == '__main__':
    # Découpons notre base de données en deux.
    # Une partie pour l'entraînement du réseau, l'autre pour vérifier
    # sa performance.
    X, Y = load_mnist_data()
    X_train, Y_train = X[:60000], Y[:60000]
    X_test, Y_test = X[60000:], Y[60000:]

    net = Network(input_dim=784)
    net.add_layer(200)
    net.add_layer(10)

    accuracy = net.evaluate(X_test, Y_test)
    print('Performance initiale : {:.2f}%'.format(accuracy * 100.0))

Évaluons la performance du modèle initial. Notez qu'au premier lancement, il faudra télécharger la base mnist et que pour les bouseux (comme moi) qui ont une connexion un peu lente, quelques minutes seront peut-être nécessaires.

$ python mnist.py
Performance initiale: 10.05%

Un peu d'algèbre linéaire

Le code qui précède me semble raisonnablement explicite, sauf peut-être en ce qui concerne la manière dont sont réalisées les agrégations / activations de données d'une couche à l'autre.

Revenons un moment sur la manière dont une couche de neurones convertit une entrée en sortie.

Les données en entrée (qu'il s'agisse de la couche précédente ou des données initiales) sont constituées de 3 valeurs.

$$ X = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} $$

La couche de neurones que nous considérons est constituée de s = 5 neurones. Chaque neurone est connecté à n = 3 entrées. Ce qui nous donne un total de s x n = 15 poids.

On note généralement les poids w_ij ou j est l'indice de l'entrée et i l'indice du neurone.

w₁₂ est donc le poids qui relie la deuxième entrée au premier neurone de la couche.

On note généralement tous les poids de la couche dans une seule matrice.

$$ W = \begin{pmatrix} - & W_{1} & - \\ - & W_{2} & - \\ & \tiny{\vdots} \\ - & W_{s} & - \end{pmatrix} = \begin{pmatrix} w_{11} & w_{12} & \cdots & w_{1n} \\ w_{21} & w_{22} & \cdots & w_{2n} \\ & & \tiny{\ddots} \\ w_{s1} & w_{s2} & \cdots & w_{sn} \end{pmatrix} $$

Les biais sont également stockés dans une matrice.

$$ B = \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_s \end{pmatrix} $$

Rappelons la formule qui permet de calculer la réponse d'un seul neurone :

$$\sigma(\sum_{i=1}^{n} w_ix_i + b)$$

Le résultat que nous souhaitons obtenir, que nous noterons Y, est donc le suivant :

$$ Y = \begin{pmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{s} \end{pmatrix} = \begin{pmatrix} \sigma(\sum_{i=1}^{n} w_{1i}x_i + b_1) \\ \sigma(\sum_{i=1}^{n} w_{2i}x_i + b_2) \\ \vdots \\ \sigma(\sum_{i=1}^{n} w_{si}x_i + b_s) \end{pmatrix} = \begin{pmatrix} \sigma(w_{11}x_1 + w_{12}x_2 + \cdots + w_{1n}x_n + b_1) \\ \sigma(w_{21}x_1 + w_{22}x_2 + \cdots + w_{2n}x_n + b_2) \\ \vdots \\ \sigma(w_{s1}x_1 + w_{s2}x_2 + \cdots + w_{sn}x_n + b_s) \end{pmatrix} $$

Comment implémente-t-on ce calcul ? Il serait tout à fait possible de procéder avec une bête boucle imbriquée.

Y = []
for s in range(nb_neurons):
    line_sum = 0
    for n in range(input_size):
        line_sum += weights[s][n] * X[n]
    line_sum += biases[s]
    Y.append(sigmoid(line_sum))

Mais quelle inefficacité ! Multipliez ça par le nombre de couches, et vous verrez qu'il faut un temps infini (à l'échelle d'un processeur, tout du moins) pour propager les données de la première à la dernière couche.

Il s'avère qu'il existe un moyen beaucoup plus élégant et efficace pour arriver au même résultat : l'algèbre linéaire et le calcul matriciel. Je vous laisse réviser rapidement le principe des opérations sur les matrices, mais pour les paresseux, voici un rapide résumé.

$$ A = \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{pmatrix} B = \begin{pmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \end{pmatrix} $$

$$ A * B = \begin{pmatrix} a_{11}b_{11} + a_{12}b_{21} & a_{11}b_{12} + a_{12}b_{22} & a_{11}b_{13} + a_{12}b_{23} \\ a_{21}b_{11} + a_{22}b_{21} & a_{21}b_{12} + a_{22}b_{22} & a_{21}b_{13} + a_{22}b_{23} \\ a_{31}b_{11} + a_{32}b_{21} & a_{31}b_{12} + a_{32}b_{22} & a_{31}b_{13} + a_{32}b_{23} \\ \end{pmatrix} $$

L'algèbre linéaire stipule que :

$$ W * X + B = \begin{pmatrix} w_{11} & w_{12} & \cdots & w_{1n} \\ w_{21} & w_{22} & \cdots & w_{2n} \\ & & \tiny{\ddots} \\ w_{s1} & w_{s2} & \cdots & w_{sn} \end{pmatrix} * \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} + \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_s \end{pmatrix} $$

$$ = \begin{pmatrix} w_{11}x_1 + w_{12}x_2 + \cdots + w_{1n}x_n + b_1 \\ w_{21}x_1 + w_{22}x_2 + \cdots + w_{2n}x_n + b_2 \\ \tiny{\ddots} \\ w_{s1}x_1 + w_{s2}x_2 + \cdots + w_{sn}x_n + b_s \end{pmatrix} $$

Numpy dispose de primitives optimisées pour réaliser ce genre de calculs. Ainsi, on peut écrire en python :

aggregation = np.dot(W, X) + B

Qui plus est, numpy est suffisamment intelligent pour appliquer une fonction élément par élément quand on lui passe un vecteur. Par conséquent, calculer le résultat de toute la couche se fait en une seule ligne et de manière optimisée :

Y = sigmoid(np.dot(W, X) + B)

La vie n'est-elle pas belle ?

À quoi sert-ce ?

« Oulala ! tout ça c'est bien gentil, mais puisque de toutes façons je n'aurai jamais besoin d'implémenter ça moi-même, à quoi sert-il que l'on en rajoute à ma charge cognitive avec des optimisations à base de matrices et autres joyeusetés ? » C'est peut-être votre état d'esprit en ce moment, c'était en tout cas le mien au début.

Puisque le code que nous implémentons aujourd'hui n'est que pédagogique et que nos petites optimisations n'atteindront jamais la performance des outils dédiés, il est vrai que nous aurions pu aller au plus simple et nous éviter de devoir réviser les opérations matricielles.

J'en parle néanmoins parce que dans à peu près tous les articles, tous les billets, toute la littérature intéressante sur le sujet, les auteur·e·s utilisent les notations matricielles. Par conséquent, ça me parait un concept intéressant à appréhender pour se former au deep learning.

Et dans la mesure ou le machine learning fait souvent appel à la parallélisation des calculs, la vectorisation est un concept intéressant à ajouter à sa boîte à outils.

Cet algo qui nous traîne et nous entraîne

Bien bien bien… Nous avons un modèle, qui est pour l'instant inutile puisqu'il réalise des prédictions aléatoires. Il est temps pour nous de faire tourner l'algo d'apprentissage.

Ou pas. Car ce billet commence à être fichtrement long et j'aimerais partir en week-end. Nous verrons donc comment fonctionne l'algorithme d'entraînement pour un tel modèle la prochaine fois.