Un peu de crypto avec les courbes elliptiques
Dans ce billet assez technique, nous allons étudier un outil mathématique poétiquement intitulé les « courbes elliptiques ». Même si vous ne savez pas ce que sont les courbes elliptiques, vous en avez utilisé sans le savoir, car elles constituent l'un des fondements de la cryptographie moderne. Accrochez-vous.
Les opérations sur les courbes elliptiques sont utilisées dans la cryptographie asymétrique et notamment par l'algorithme ECDSA (Elliptic Curve Digital Signature Algorithm).
Par rapport à RSA (par exemple), qui utilise les multiplications de nombre premiers, ECDSA offre un meilleur niveau de sécurité à taille de clé équivalente. Les opérations de signature sont de plus beaucoup plus rapides, même si en revanche leur vérification est un peu plus lente.
ATTENTION : dans ce billet, je parle de mathématiques, ce n'est pas ma spécialité ; je manie allègrement l'approximation, soit dans un but pédagogique, soit parce que cette approximation reflète celle de ma propre compréhension. Amis mathématiciens, si vous repérez quelques énormités, ne vous étouffez pas ; envoyez moi plutôt un petit message et je m'amenderai.
Qu'est-ce qu'une courbe elliptique ?!
Une courbe elliptique n'est rien d'autre qu'une représentation d'une équation de la forme :
y 2 = x 3 + ax + b
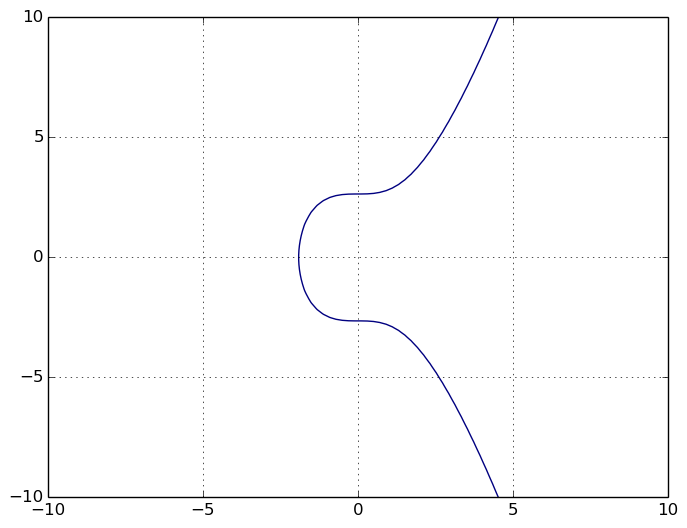
où a et b sont des nombres réels. Voici une chouette représentation graphique pour que vous ayez une idée de la gueule que ça peut avoir :
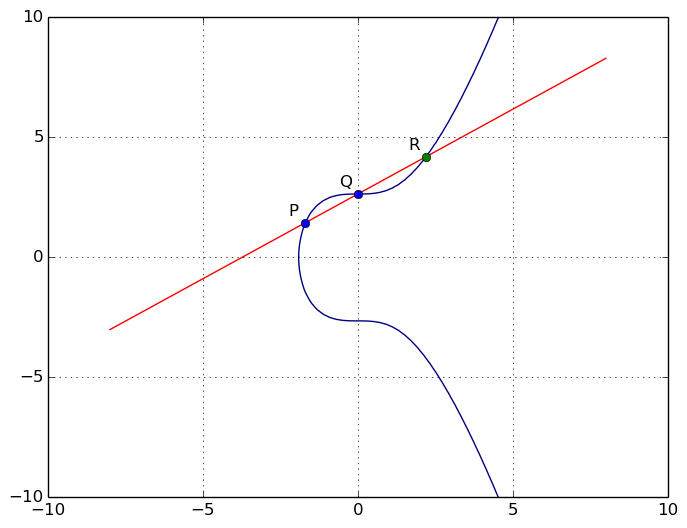
Une propriété fort intéressante de ce type de courbes et qu'une droite qui coupe notre courbe en deux points passe forcément par un troisième point (sauf exceptions que nous allons voir plus loin).
Courbes elliptiques et champs finis
Les courbes que vous avez vu jusqu'à maintenant ne sont pas directement utilisables dans un contexte cryptographique. Nous allons apporter deux modifications essentielles.
- D'abord, nous allons uniquement travailler avec des entiers. Nous ne garderons donc que les points dont l'abscisse et l'ordonnée sont des entiers.
- Nous allons utiliser l'arithmétique modulaire pour limiter l'abscisse et l'ordonnée maximale de chaque point. À une courbe, on ajoute donc un nouveau paramètre P, et chaque point sera exprimé modulo P.
Voici un exemple de courbe elliptique qui répond à ces propriétés, avec P = 97 :
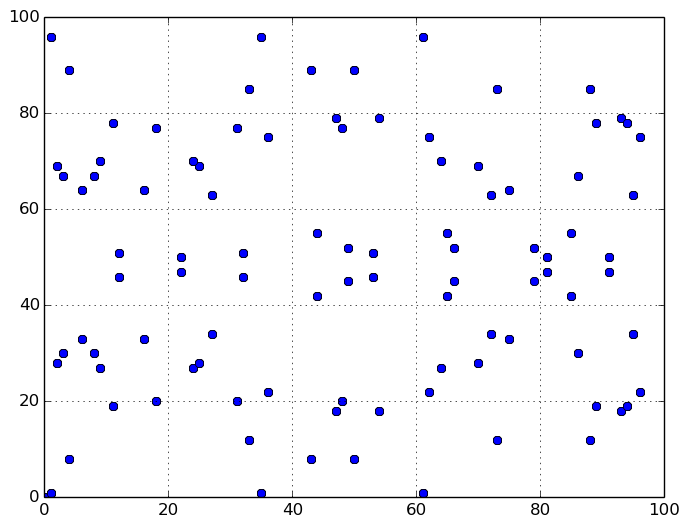
Évidemment, ça ne ressemble plus vraiment à une courbe, mais on s'en fout. L'important, c'est de garder à l'idée que cette « chose » conserve toutes les propriétés qui nous intéressent.
Et puis notez aussi qu'en pratique, P est un petit peu plus grand que 97. Quelque chose comme 115792089237316195423570985008687907853269984665640564039457584007908834671663, par exemple.
Le point à l'infini
En plus des points de la courbe, il nous faut définir un point « à l'infini » que nous nommerons affectueusement « 0 ». Grosso-modo, prenez tous les points de la courbe, pour chaque point, tracez une droite verticale : notre « 0 » se trouve au point de croisement de toutes ces droites.
Ça demande un bon niveau en maths ou un peu d'imagination. Nous allons voir l'utilité de ce point un peu plus loin.
Un peu de Python
Une courbe elliptique peut être représentée en Python de la manière la plus simple qui soit :
class EllipticCurve(object):
"""Represents a single elliptic curve defined over a finite field.
See here:
http://en.wikipedia.org/wiki/Elliptic_curve
http://jeremykun.com/2014/02/24/elliptic-curves-as-python-objects/
p must be prime, since we use the modular inverse to compute point
addition.
"""
def __init__(self, a, b, p):
self.a = a
self.b = b
self.p = p
def __eq__(self, C):
return (self.a, self.b) == (C.a, C.b)
def has_point(self, x, y):
return (y ** 2) % self.p == (x ** 3 + self.a * x + self.b) % self.p
def __str__(self):
return 'y^2 = x^3 + {}x + {}'.format(self.a, self.b)
Un point de la courbe n'est pas beaucoup plus complexe :
class Point(object):
"""A point on a specific curve."""
def __init__(self, curve, x, y):
self.curve = curve
self.x = x % curve.p
self.y = y % curve.p
if not self.curve.has_point(x, y):
raise ValueError('{} is not on curve {}'.format(self, self.curve))
def __str__(self):
return '({}, {})'.format(self.x, self.y)
def __getitem__(self, index):
return [self.x, self.y][index]
def __eq__(self, Q):
return (self.curve, self.x, self.y) == (Q.curve, Q.x, Q.y)
def __neg__(self):
return Point(self.curve, self.x, -self.y)
Nous traitons à part le cas du point 0 :
class Inf(Point):
"""The custom infinity point."""
def __init__(self, curve):
self.curve = curve
def __eq__(self, Q):
return isinstance(Q, Inf)
def __neg__(self):
"""-0 = 0"""
return self
Addition et multiplication
Maintenant que nous avons notre courbe, nous allons faire quelque chose que certains appellent des « mathématiques » mais qu'à mon niveau j'ai du mal à distinguer de la magie pure : nous allons définir une opération totalement arbitraire, vérifier qu'elle répond à toute les propriétés mathématiques d'une addition, ce qui nous autorisera à appeler cette opération « addition », tout simplement.
Prenez deux points P et Q sur une courbe C. Tracez la droite D qui passe par P et Q. Soit R le troisième point d'intersection entre D et C. Soit R' le symétrique de R par rapport à l'axe des abscisse. Le Grand Dieu des maths nous autorise à énoncer que :
P + Q = R'
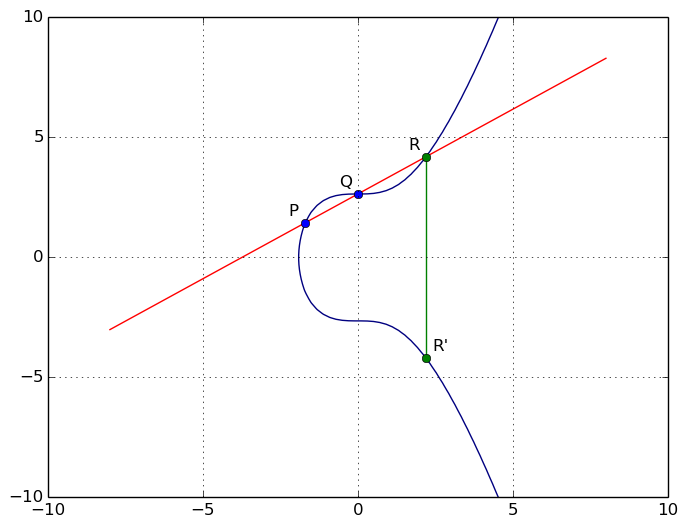
Voilà, vous savez maintenant comment on additionne deux points sur une courbe elliptique. Cool, non ?! Par contre, il nous reste quelques cas particuliers à traiter.
Si la droite ne passe en fait que par deux points de la courbe parce qu'elle lui est tangente, on considère le point de tangente comme deux points distincts, et on fait comme d'habitude : P + P = Q', P + Q = P'.
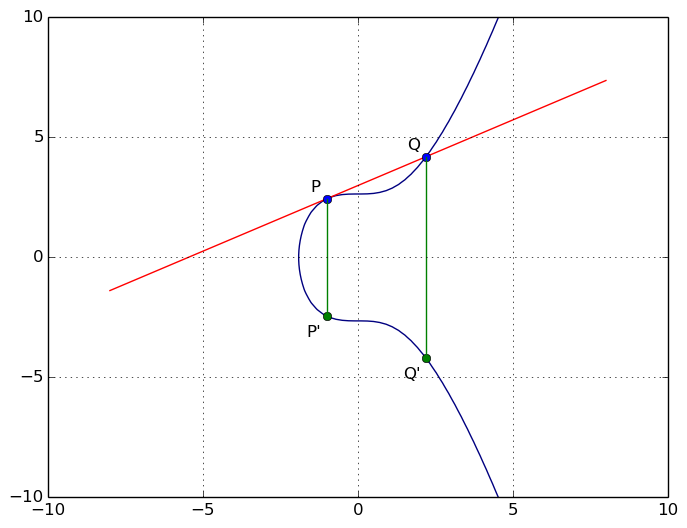
Si la droite qui passe par P et Q est verticale, alors le troisième point se trouve à l'infini. Il s'ensuit que P + Q = 0.
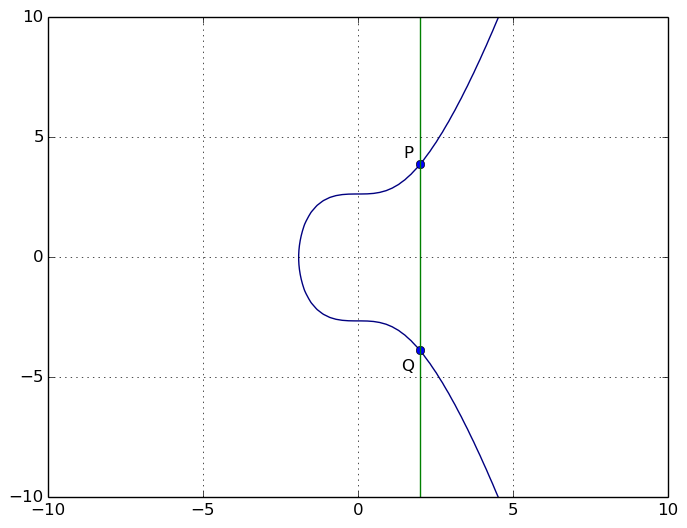
Ça vaut aussi si P = Q.
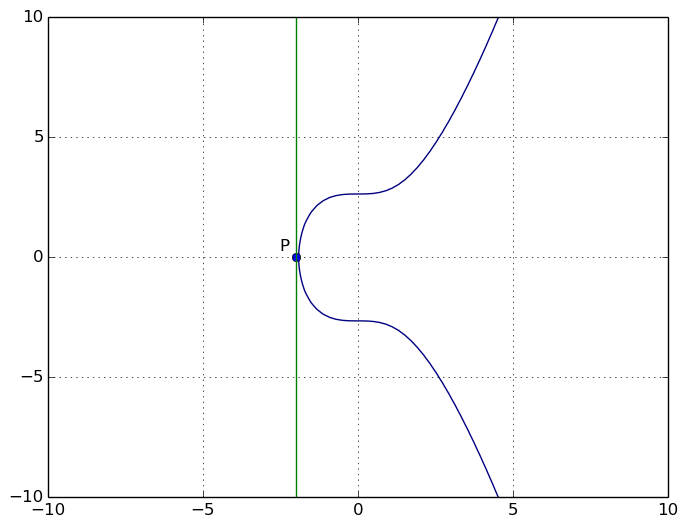
Maintenant, vous pouvez vous amuser vous même à vérifier que les propriétés suivantes sont bien vérifiées.
- P + Q = Q + P
- (P + Q) + R = P + (Q + R)
- P + 0 = P
Par ailleurs, on remarque que P + P' = 0. On peut donc noter P' « -P » et définir dans la foulée l'opération de soustraction : P - Q = P + (-Q). Tant qu'à faire, on définit la multiplication n * P avec n étant un entier comme P + P + … + P (n fois).
Préparez l'aspirine
Tout ceci est bel et bon, mais comment additionne-t-on concrètement deux points ? C'est là que ça commence un peu à se corser. Les formules nous sont gentiment données par Wikipédia.
Si on additionne deux points distincts, P + Q = R.
$$λ = \frac{y_q - y_p }{ x_q - x_p}$$
$$x_r = λ^2 - x_p - x_q$$
$$y_r = λ (x_p - x_r) - y_p$$
Si on additionne (double) un point avec lui-même, P + P = R.
$$λ = \frac{3 x_p^2 + a }{ 2 y_p }$$
$$x_r = λ^2 - 2 x_p$$
$$y_r = λ (x_p - x_r) - y_p$$
Ou a est le a de l'équation de la courbe.
Ces formules ne sont pas tirées d'un chapeau, mais nous n'allons pas rentrer dans les détails.
Voici l'implémentation Python de ces formules.
class Point(object):
…
def __add__(self, Q):
"""Add two points together.
We need to take care of special cases:
* Q is the infinity point (0)
* P == Q
* The line crossing P and Q is vertical.
"""
assert self.curve == Q.curve
# 0 + P = P
if isinstance(Q, Inf):
return self
xp, yp, xq, yq = self.x, self.y, Q.x, Q.y
m = None
# P == Q
if self == Q:
if self.y == 0:
R = Inf(self.curve)
else:
m = ((3 * xp * xp + self.curve.a) * mod_inverse(2 * yp, self.curve.p)) % self.curve.p
# Vertical line
elif xp == xq:
R = Inf(self.curve)
# Common case
else:
m = ((yq - yp) * mod_inverse(xq - xp, self.curve.p)) % self.curve.p
if m is not None:
xr = (m ** 2 - xp - xq) % self.curve.p
yr = (m * (xp - xr) - yp) % self.curve.p
R = Point(self.curve, xr, yr)
return R
class Inf(Point):
def __add__(self, Q):
"""P + 0 = P"""
return Q
Mmm… Du beau code bien touffu comme on l'aime…
Bon, je sens que vous commencez à fatiguer, alors voici une belle image bucolique pour vous reposer un peu les yeux. Faites moi signe quand vous serrez prêt à reprendre.
C'est bon, on peut y aller ?
Les plus attentifs d'entre vous (je sais qu'il y en a) auront remarqués que nous avons remplacé toutes les opérations de division par la multiplication par l'inverse modulaire. Je vous laisse vous renseigner vous même si vous le souhaitez, moi je sature. Parce que je ne suis pas vache, je vous donne quand même l'implémentation…
def mod_inverse(a, n):
"""Return the inverse of a mod n.
n must be prime.
>>> mod_inverse(42, 2017)
1969
"""
b = n
if abs(b) == 0:
return (1, 0, a)
x1, x2, y1, y2 = 0, 1, 1, 0
while abs(b) > 0:
q, r = divmod(a, b)
x = x2 - q * x1
y = y2 - q * y1
a, b, x2, x1, y2, y1 = b, r, x1, x, y1, y
return x2 % n
La multiplication elliptique
Comment calculer n * P ? L'approche naïve serait d'opérer une succession d'addition.
P + P + … + P (n fois)
Je vous laisse imaginer l'efficacité déplorable d'une telle opération. Heureusement, il existe d'autres moyens plus efficaces, et c'est d'ailleurs la raison pour laquelle la cryptographie via courbes elliptiques peut fonctionner.
L'algorithme classique s'appelle « double and add » et comme son nom l'indique, nous allons procéder par succession de point doubling et d'additions.
Convertissons n dans sa représentation binaire. Par exemple avec n = 19 :
$$19 = 0b10011 = 16 + 2 + 1 = 2^4 + 2^1 + 2^0$$
Maintenant, notez que :
$$19 P = 2^4 P + 2^1 P + 2^0 P = 2(2(2(2(P)))) + 2(P) + P$$
On calcule ainsi 19P en deux additions et cinq doubling* au lieu de 18 additions. (O(lg_2 n)), ça vous parle ?
class Point(object):
…
def __mul__(self, n):
assert isinstance(n, (int, long))
assert n > 0
n = n % self.curve.p
if n == 0:
return Inf(self.curve)
else:
Q = self
R = Inf(self.curve)
i = 1
while i <= n:
if n & i == i:
R = R + Q
Q = Q + Q
i = i << 1
return R
def __rmul__(self, n):
return self * n
Clé publique, clé privée
Pfiiiou… Nous pouvons nous autoriser un petit soupir de soulagement. Néanmoins, nous n'avons fait que parler d'arithmétique. Où est la crypto là dedans ? Nous n'avons toujours pas généré de couple de clés publique / privée, par exemple. Soit, nous allons y remédier.
Soient les paramètres (A, B, P, G, n) tels que :
- La courbe C définie par : (y^2 = x^3 + Ax + B (mod P))
- G un point de la courbe
- n le nombre entier tel que n * G = 0
Toutes les courbes ne se valent pas, et ces paramètres ne sont pas choisis au hasard. Plusieurs courbes sont proposées par le Standards for Efficient Cryptography Group (SECG). Le protocole Bitcoin, par exemple, utilise la courbe poétiquement nommée « secp256k1 » dont les paramètres sont les suivants :
P = 2 ** 256 - 2 ** 32 - 2 ** 9 - 2 ** 8 - 2 ** 7 - 2 ** 6 - 2 ** 4 - 1
A = 0
B = 7
GX = 0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
GY = 0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8
G = (GX, GY)
N = 0XFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
Pour générer une clé privée, il suffit de choisir au hasard un nombre s entre 1 et N - 1. Facile, non ? La clé publique, quand à elle, est égale au point Q = s * G.
Connaissant s et G, vous savez désormais qu'il est très facile de calculer Q. En revanche, il est virtuellement impossible de retrouver s à partir de G et Q. Du moins, pas sans disposer de quelques millions d'années devant vous.
Signature d'un message
L'algorithme ECDSA (Elliptic Curve Digital Signature Algorithm) permet de signer des messages ; en lui même, il n'a pas grand intérêt, donc pas la peine d'en faire des tartines.
Imaginez que vous souhaitiez signer quelque chose, n'importe quelle suite de bits (une phrase, un fichier, on s'en fout). Voici comment on signe ce bazar avec la courbe (A, B, P, G, n) :
- (m = H(message)) ou H est un algo de hash, par exemple SHA-256.
- Soit k un entier au hasard entre 1 et n - 1
- Soit r l'abscisse du point k * G (mod n)
- Soit s = k-1 (m + kr) (mod n)
La signature est donnée par le couple r, s.
class ECDSA(object):
def __init__(self, curve, generator, order):
self.curve = curve
self.G = generator
self.n = order
def sign(self, msghash, privkey):
msg = bytes_to_int(msghash)
k = randint(1, self.n - 1)
i, j = k * self.G
r = i % self.n
s = (mod_inverse(k, self.n) * (msg + r * privkey)) % self.n
return r, s
Vérification d'une signature
Idem, le processus de vérification de la signature est relativement simple. Soient m notre hash de message, et la signature (r, s).
- Vérifier que la clé publique Q est valide.
- Vérifier que n * Q = 0.
- Vérifier que r et s sont dans [1, n - 1]
- w = s-1 (mod n)
- (i, j) = m * w * G + r * w * Q
- Si i = r (mod n), alors la signature est valide
Quelques références
Merci d'avoir tout lu jusque là. Je vous laisse, je vais avaler la boite d'aspirine. Pour ceux qui veulent aller plus loin, je vous laisse quelques liens à consulter.
- http://en.wikipedia.org/wiki/Elliptic_curve
- http://en.wikipedia.org/wiki/Elliptic_curve_cryptography
- http://en.wikipedia.org/wiki/Elliptic_Curve_DSA
- http://jeremykun.com/2014/02/24/elliptic-curves-as-python-objects/
- http://jeremykun.com/2014/02/08/introducing-elliptic-curves/ (ce blog est une pure mine d'or)
- http://blog.cloudflare.com/ecdsa-the-digital-signature-algorithm-of-a-better-internet