Comprendre la musique
J'écoute de la musique, et j'aime ça ; mais je n'y connais rien à la musique. Un jour, je me suis dit « tiens, ça serait cool d'essayer d'écrire de la musique ». J'ai ouvert un nombre incalculables de sites et livres portants sur la théorie musicale, et je les ai refermés avec l'impression d'être un parfait demeuré.

La plupart des ouvrages qui parlent de théorie musicale semblent présupposer que les lecteur·ice·s maîtrisent déjà… la théorie musicale. Ce qui est franchement con, vous en conviendrez.
Après avoir galéré pendant pas mal de temps, je vais tâcher d'écrire le billet que j'aurais aimé lire quand j'ai commencé, à l'usage de celles et ceux qui n'ont aucune base mais voudraient comprendre la musique.
Qu'est-ce que la musique ?
La musique, c'est simplement du bruit avec des trous dedans. Le tout étant censé être agréable à entendre. « Agréable » étant un jugement subjectif, son appréciation est laissée aux lecteur·ices.
La musique est un art très ancien, sans doute aussi vieux que l'humanité elle-même. Ses fondements reposent sur des éléments concrets et objectifs, à savoir les lois de la physique et le fonctionnement de notre audition.
Ceci étant dit, l'audition, comme la vue ou le goût, est une sensation, donc une part de psychologique entre en jeu. Il est possible d'apprendre à apprécier (dans une certaine mesure) une sensation auditive qui auparavant nous semblait désagréable. La musique étant pratiquée depuis si longtemps, il est normal que ce soit développée une forte culture, c'est à dire un ensemble de règles plus ou moins arbitraires mais communément admises.
Écouter et apprécier de la musique est ainsi facile et instinctif (plus ou moins, certains genres musicaux plus élaborés peuvent nécessiter un peu plus d'apprentissage, mais même si je n'apprécie pas vraiment un concerto de Mozart, je sais qu'il s'agit de musique), à la fois parce que notre audition fonctionne d'une façon donnée, à la fois parce que nous baignons pour la plupart depuis notre naissance dans une certaine culture musicale.
En revanche, s'initier à la théorie musicale moderne (c'est à dire se conformer à l'état de l'art en matière de création musicale, être capable de lire et d'écrire la notation musicale moderne) nécessite d'appréhender de nombreuses pratiques, codes, règles, notations, concepts… qui ont évolués et se sont affinés lentement au fil des siècles, parfois pour des raisons concrètes, parfois pour des motifs plus ou moins arbitraires.
Par ailleurs, la plupart des ouvrages musicaux sont assez avares d'explications concrètes sur les origines et raisons des nombreuses règles qu'ils présentent. On nous explique qu'il y a sept notes (do, ré, mi, fa, sol, la, si), mais rarement pourquoi pas cinq ou quarante-deux.
Dans ce billet, nous allons tâcher de partir du concret pour mieux comprendre pourquoi la théorie musicale est ce qu'elle est aujourd'hui.
Le son
La base de la musique, c'est le son.
Un son est une sensation provoquée par une vibration de l'air. Les vibrations se propagent d'un milieu à l'autre. Si vous tapez sur un truc, il va vibrer, ce qui fera vibrer l'air, qui fera vibrer un petit bitoniau au fond de votre oreille, ce que votre cerveau traduira par une sensation de « bloïng » ou « flapf » (en fonction de ce sur quoi vous aurez tapé).
Nous avons déjà évoqués les ondes lorsque nous avons disserté de la couleur. Une des propriétés d'une onde, c'est sa fréquence. On l'exprime en hertz (Hz), qui est une manière raccourcie de dire « par secondes ».
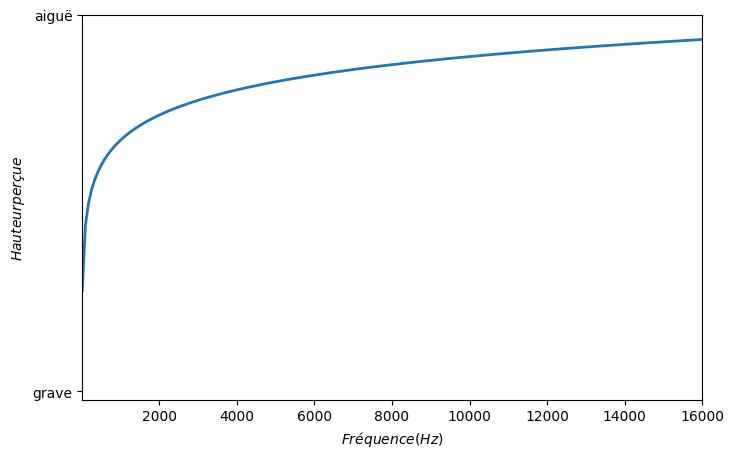
La fréquence est ce qui détermine la hauteur du son. Plus l'air vibre vite (plus la fréquence du son en Hz est élevée), plus nous aurons tendance à interpréter le son comme « aigüe ».
Il est important de noter que la relation entre fréquence et hauteur n'est pas linéaire. Ainsi, mon oreille percevra une grande différence entre deux sons de 100 Hz et 200 Hz, mais très peu entre 10000 Hz et 10100 Hz.
Un instrument de musique, c'est donc un machin qu'on peut faire vibrer en tapant dessus, soufflant dedans, en le caressant, ou que sais-je… et dont on peut moduler la fréquence de vibration pour produire un son plus ou moins aigüe.
Notes et consonance
Les premiers instruments de musiques étaient sans doute assez basiques. Je n'ai pas d'informations là dessus mais j'imagine assez bien un humain des cavernes bas du front danser en slip en tapant en cadence à coup de silex sur le crâne séché de l'ancien chef d'une tribu récemment conquise. Mais en ce temps là, les distractions étaient rares et les instruments à une seule note ont probablement rapidement montré leurs limites en terme de potentiel de divertissement.
Pour produire des mélodies, il faut… plusieurs notes (quoique certains se débrouillent avec une seule… voire zéro) !Assez rapidement, notre sympathique musicien des cavernes et ses descendants se sont rendus comptes que certaines notes (certaines fréquences), jouées en séquence ou simultanément, sonnaient juste, tandis que d'autres non. Mais avant de se demander pourquoi certaines fréquences sonnent juste et d'autres non, il faut tâcher de comprendre ce que signifie « sonner juste ». Ce qui nous amène au concept de consonance.
Si vous jouez simultanément un gros tas de notes au hasard, par exemple en donnant un coup de pied dans une caisse remplie de vaisselle ou en vous tapant le crâne sur le clavier d'un piano, il y a des chances que la sensation auditive qui en résulte soit désagréable (d'autant plus si elle s'accompagne de la douleur provoquée par un orteil cassé), on parle de dissonance. Alors qu'en sélectionnant vos notes avec soin, vous avez une chance d'obtenir une sensation agréable, et on parle de consonance. La meilleure explication de la consonance que j'ai trouvée provient de la théorie de la musique de A. Danhauser.
Les intervalles consonants sont ceux que forment ensemble deux sons que l'oreille n'éprouve pas le besoin de séparer ; la consonance donne une impression d'unité, de cohésion et de stabilité.
Les intervalles dissonants, au contraire, sont ceux que forment entre eux deux sons que l'oreille éprouve le besoin de modifier, en les remplaçant par d'autres sons ; la dissonance donne une impression d'instabilité […].
En gros, lorsque vous jouez simultanément plusieurs notes consonantes, votre cerveau va percevoir un seul son, plus riche et plus complexe que les notes individuelles qui le composent ; lorsque vous jouez des notes dissonantes, votre cerveau s'aperçoit qu'il y a plusieurs sons et s'attache à bien les séparer pour que vous les perceviez comme tels.
J'imagine que la raison de ce fonctionnement est évolutive. Pour survivre dans la jungle ancestrale, il fallait être capable de percevoir le délicat froufrou du prédateur qui approche dans les hautes herbes malgré les ronflements tonitruants de ses voisins de chambrée troglodyte.
La notion de consonance est fondamentale pour comprendre la théorie musicale. Mais alors, qu'est-ce qui fait que deux (ou plus) notes soient ou non consonantes ?
La suite harmonique
Pour mieux comprendre pourquoi certains sons sont consonants, il faut mieux comprendre ce qui compose un son. Ce qui nous amène à un concept qui porte le joyeux nom de suite harmonique.
Quizz ! Qu'est-ce qu'une suite harmonique ?
- A. Une chambre d'hôtel particulièrement bien décorée.
- B. Une main gagnante au poker.
- C. Une sequel qui reprend juste à la fin du film précédent.
- D. Une série d'ondes superposées qui composent un son.
Imaginons une corde de ukulélé dont la composition, la longueur et la tension sont réglés pour vibrer 440 fois par secondes, donc à 440 Hz. En tirant la corde, on l'éloigne de sa position de repos. Quand on la relâche, du fait de son élasticité, elle va se mettre à osciller autour de la position de repos (440 fois par secondes, donc).
Si on filmait la corde en gros plan et au ralenti, on s'attendrait sans doute à voir quelque chose comme ça :
Or, si c'était bien le cas, le son produit serait le suivant :
Que je sois privé de crêpes pendant une semaine si vous trouvez un instrument qui sonne ainsi.
Si le son d'une ukulélé est différent de la tonalité que vous entendez quand vous décrochez votre téléphone, c'est parce que sa corde, toujours au ralenti, ressemble plutôt à ça :
La corde est déformée par une vibration principale, mais également par toute une série de vibrations secondaires, chacune avec une longueur d'onde et une fréquence différente, qui se superposent.
Si on utilisait un procédé mathématique pour isoler les ondes et les disposer côte-à-côte, on obtiendrait quelque chose comme ça :
Comprendre pourquoi la corde agit ainsi nécessiterait de suivre un cours sur la physique ondulatoire, domaine que je ne maîtrise pas et qui nous amènerait un peu loin. Je vous demanderai donc de vous contenter de me croire sur parole, ou de faire vos propres recherches.
Observez maintenant la dernière vidéo, et tâchez de repérer la relation entre les fréquences d'oscillation de ces différentes ondes.
Vous trouvez ?
Ok, je vous aide…
Quand la première onde oscille une fois (un aller-retour), la deuxième onde oscille… deux fois. La troisième oscille trois fois, la quatrième quatre fois, etc.
Quand je pince une corde de guitare, et c'est à peu près vrai pour tous les sons présents dans la nature, le son résultant est toujours composé d'une série de vibrations superposées. La vibration principale est nommée la fondamentale : c'est la plus audible, et c'est elle qui détermine la hauteur du son. Les vibrations suivantes dans la suite sont nommée harmoniques et ont pour fréquence un multiple entier de la fréquence fondamentale.
| Rang | Fréquence (Hz) | Relation par rapport à la fondamentale |
|---|---|---|
| 1 | 440 | NA |
| 2 | 880 | 2 * 440 |
| 3 | 1320 | 3 * 440 |
| 4 | 1760 | 4 * 440 |
| 5 | 2200 | 5 * 440 |
| … | … | … |
Quelque soit la fréquence fondamentale, les fréquences suivantes sont toujours liées par ce même rapport.
Toutes les harmoniques d'une suite n'ont pas forcément la même amplitude, c'est à dire que pour un son donné, certaines fréquences seront plus ou moins audibles. La suite est théoriquement infinie, mais globalement, plus on avance dans la suite, moins l'harmonique est audible.
C'est la composition de cette suite (c'est à dire à quel point une harmonique donnée est plus ou moins audible en fonction des autres) qui donne à un son donné son timbre, et c'est ce qui permet de distinguer le son de deux instruments produisant la même note.
Pour info, certains algorithmes de compression sonore fonctionnent en supprimant du signal audio les harmoniques les moins audibles.
Harmonique et consonance
En quoi cette suite harmonique est-elle liée à la notion de consonance ?
D'abord, j'imagine qu'il y a là un effet psychologique. Toute notre évolution a calibré notre audition pour que lorsque nous percevions plusieurs vibrations dont les longueurs d'ondes sont liées entre elles par un facteur entier, notre cerveau nous dise « je viens de recevoir un gros paquet de vibrations mais t'inquiètes pas pépère, je t'ai fait un petit mémo qui résume tout ça. ». Un seul et même son.
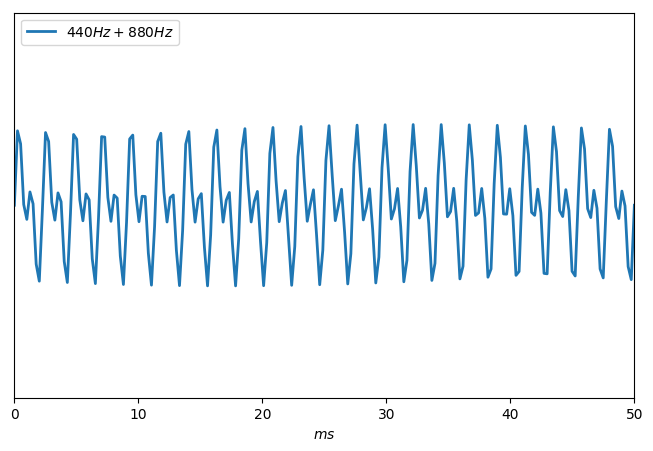
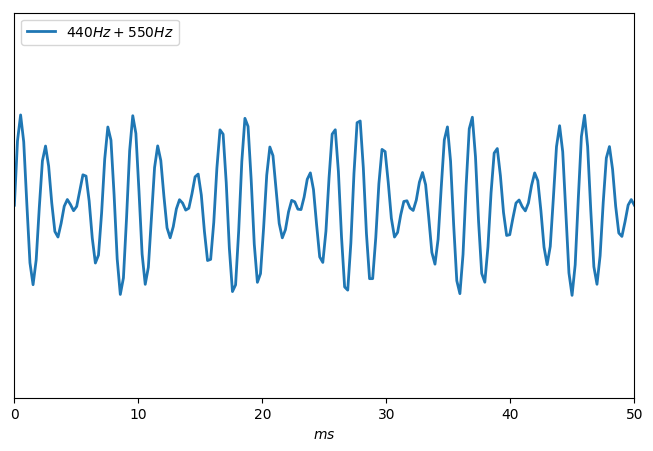
Mais la consonance peut aussi se mesurer à des éléments concrets. Ainsi, voici la tronche de l'onde observée si je superpose deux vibrations de fréquences respectives 440 Hz et 880 Hz.
Notez que la courbe obtenue est parfaitement stable dans le temps, nonobstant de bizarres approximations provoquées par mon outil de rendu.
À l'oreille, il est pratiquement impossible de distinguer les deux vibrations l'une de l'autre (en tout cas, moi je n'y arrive pas).
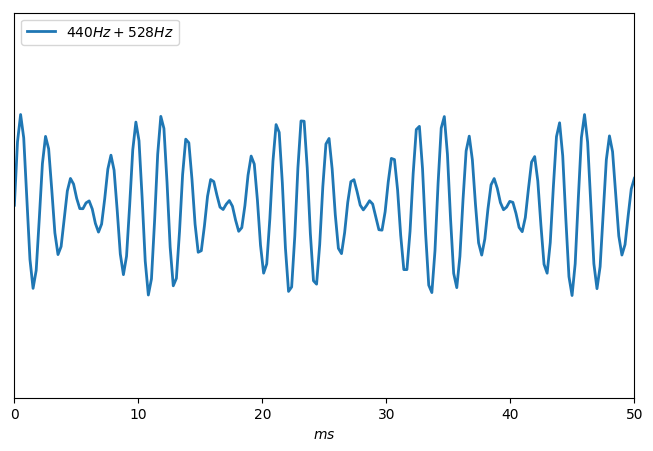
Voici maintenant ce qui se passe si j'utilise les fréquences de 440 Hz et 528 Hz, dont la dissonance relative est avérée.
Notez que la superposition de ces deux ondes ne produit pas un résultat stable, on observe des variations d'amplitude, que l'oreille perçoit comme un « battement » désagréable. Plusieurs exemples de battements sur l'article (en) de Wikipédia..
Ainsi, plus le rapport entre leurs deux fréquences est simple, plus la consonance sera forte entre deux sons simples (chacun composés d'une seule onde).
Et pour les sons complexes, les « vrais » sons, qu'on peut entendre dans la nature et qui sont composés de plusieurs harmoniques ? Et bien si leurs fréquences fondamentales sont liées par un rapport simple, il y a des chances pour que plusieurs harmoniques se recoupent et soient consonantes deux à deux, avec un résultat global plus consonant.
En résumé : un son est composé d'un gros paquet de vibrations superposées dont les fréquences sont liées entre elles par un certain rapport mathématique. Si on peut jouer deux sons simultanément et faire en sorte que la plupart des vibrations composant ces deux sons soient liées entre elles par ce même rapport, alors l'oreille considère qu'il s'agit d'un seul son, et on a une consonance.
Intervalles consonants
Nous comprenons maintenant la notion de consonance et de dissonance. En avançant dans l'étude de la série harmonique, nous pouvons mieux comprendre comment sélectionner les notes relatives pour obtenir des suites de notes consonantes.
La notion de consonance n'est pas binaire. Deux sons peuvent être plus ou moins consonants. Pour comprendre la théorie musicale actuelle, il faut étudier les premières harmoniques de la suite.
| Rang | Fréquence | Rapport avec la fréquence de l'harmonique précédente |
|---|---|---|
| 0 | 440 | NA |
| 1 | 880 | 880/440 = 2/1 = 2 |
| 2 | 1320 | 1320/880 = 3/2 = 1.5 |
| 3 | 1760 | 1760/1320 = 4/3 = 1.33… |
| 4 | 2200 | 2200/1760 = 5/4 = 1.25 |
On l'a dit, plus on avance dans la série harmonique, moins les sons sont audibles. Psychologiquement, plus petit le rang de l'harmonique, plus consonant est jugé son rapport avec l'harmonique précédent. En relisant cette phrase que je viens moi-même d'écrire, je m'aperçois que je n'y comprends rien. Procédons par l'exemple.
L'octave
Imaginons que je joue un son correspondant à une fréquence de 440 Hz. Imaginons que je joue en même temps un son correspondant à la première harmonique, dont la fréquence est 2 * 440 = 880 Hz. J'ai déjà montré l'onde résultante, mais je recolle l'image ici :
Notez comme la courbe est simple et sans fioritures. Par ailleurs, si vous faites le calcul, vous verrez que toutes les harmoniques de 880 Hz (880 * 2 = 1760, 880 * 3 = 2640…) sont également des harmoniques de 440 Hz.
Ainsi, quand deux sons sont liés entre eux par un rapport de 2 / 1, c'est à dire quand la fréquence du deuxième est égale au double de la fréquence du premier, la sensation de consonance est extrêmement forte. Tellement forte, à vrai dire, que dans la plupart des cultures musicales à travers le monde, on considère ces deux sons comme « le même ». Dans le système musical occidental, une note ayant une fréquence de 440 Hz est un « La », et une note ayant une fréquence de 880 Hz est également un « La », de même que 1760 Hz, 220 Hz, etc. On note cet intervalle l'« octave ».
La quinte
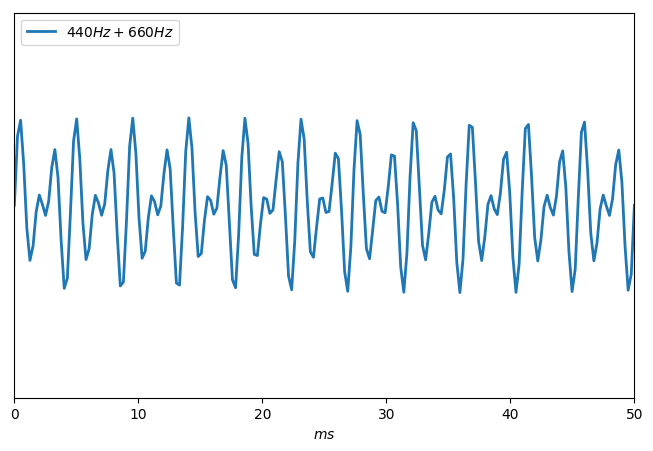
Intéressons nous maintenant à la troisième harmonique. Le rapport entre les fréquences des deuxièmes et troisièmes harmoniques est de 3 / 2, c'est à dire que 1320 / 880 = 3 / 2.
Voici la tronche de la vibration produite si je superpose deux ondes présentant cet écart :
Lorsque deux sons sont liés entre eux par ce rapport de 1.5, on parle de l'intervalle de quinte.
Notez que la courbe se complexifie un poil, mais pas tant que ça. On considère que l'intervalle de quinte est très consonant.
La quarte
Pareil pour la quatrième harmonique, avec un rapport de 4 / 3. Vous avez compris le principe.
On parle de l'intervalle de quarte.
On dit aussi que quinte et quarte sont des intervalles complémentaires dans l'octave car 3/2 * 4/3 = 2, autrement dit, si je monte d'une quinte, et encore d'une quarte, je suis en tout monté d'une octave.
La tierce
Cinquième harmonique. Rapport de 5 / 4.
On parle de l'intervalle de tierce.
Notez que la courbe se complexifie encore un peu plus. Pendant un assez long moment dans l'Histoire, l'intervalle de tierce n'a pas été considéré comme consonant.
Etc.
Vous aurez compris le principe. En avançant dans la série harmoniques, on obtient un certain nombre de rapports entre les notes qui peuvent être considérés plus ou moins consonants.
Certains chercheurs ont tenté de donner des mesures plus objectives de la consonance entre deux sons complexes, i.e composés de plusieurs harmoniques. En adaptant le code Python que d'autres ont basé sur ces travaux, on obtient la figure suivante.
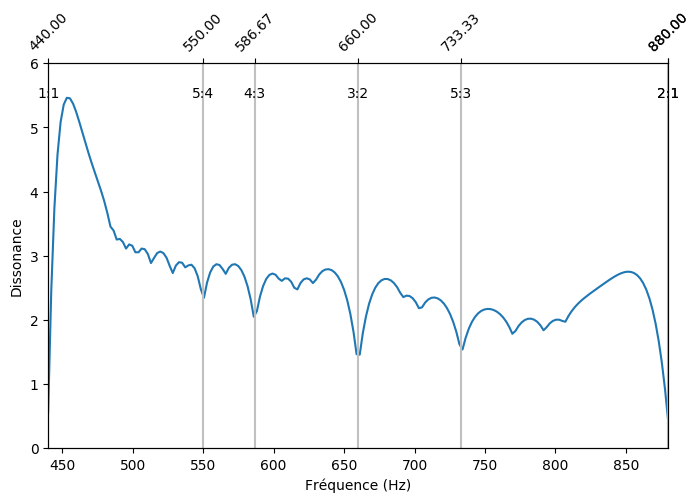
Récapitulatif
Je crois que le moment est venu de souffler un peu. Allez donc vous préparer une tisane, ensuite, on récapitulera.
Ça-y-est ? Bon ! Donc, qu'avons nous appris ?
Un son est une sensation provoquée par des vibrations dans l'air. Plus la fréquence de la vibration est importante, plus le son est perçu comme aiguë.
Chaque son naturellement produit est en fait constitué d'une multitude de vibrations, dont les fréquences sont liées entre elles par un rapport entier.
En étudiant les rapports entre ces vibrations, on peut mieux comprendre l'origine des notions de consonance et de dissonance. Deux sons sont consonants quand ils nous donnent l'impression d'entendre un seul son, plus complexe que les sons qui le composent.
La consonance n'est pas binaire. Deux sons peuvent être plus ou moins consonants.
Certains rapports simples permettent d'obtenir des sons consonants. Ainsi, deux sons séparés d'une octave (rapport de 2/1) sont considérés comme une seule et même note. D'une quinte (rapport de 3/2), très consonants. D'une tierce (5/4), plutôt consonants.
Tous ces éléments sont les mécanismes concrets et objectifs qui sous-tendent toute la (les) culture(s) musicales(s) et peuvent être déduits de l'étude d'un seul petit son. De là à dire que toutes les symphonies de Mozart sont contenues dans le tintement d'une cuiller contre un pot de Nutella, il n'y a qu'un petit pas que je vous laisse libre de franchir ou pas.
Tout ceci est bel et beau, mais savoir que deux sons sont plus ou moins consonants ne vas pas nous aider à devenir riche en composant Despacito. Il nous faut donc maintenant nous aventurer dans l'abstrait, dans le subjectif, dans le psychologique, dans la culture : étudions la théorie musicale.
Théorie musicale
Les éléments que nous avons étudiés jusqu'ici découlent des lois de la physique. Ils sont rigoureusement identiques, quelque soit votre lieu et siècle de naissance.
Mais la manière dont ces éléments ont été interprétés et utilisés pour créer ce qu'on appelle « musique », ça c'est une chose qui a différé et évolué à travers les siècles et les civilisations. Ainsi, on n'utilise pas les mêmes notes en Europe ou en Inde, et deux sons qu'on jugera plutôt consonants aux États-Unis seront jugés dissonants en Chine.
Dans ce qui va suivre, je me concentrerai sur la culture musicale occidentale, qui est probablement celle que vous connaissez, et qui a donné naissance à la Ve de Beethoven, Highway to Hell et La danse des canards.
De la nécessité de bâtir un système musical
Si vous jouez de la musique tout seul dans votre coin sur une île déserte, vous pouvez faire un peu ce que vous voulez. Mais les besoins concrets les musicien·nes à travers les âges ont rendu indispensables la création d'un système musical rigoureux.
Imaginez le premier compositeur de l'histoire, essayant d'expliquer sa musique à l'orchestre de la tribu : « Alors Gérard, tu me fais un gros pouêt bien aiguë avec ta trompette en os pendant que Géraldine enchaîne des twing twing sur sa guitare en boyaux de chèvres ». Ingérable. Pour transmettre et conserver la musique, il a bien fallu développer un système de notation musicale.
Par ailleurs, le spectre audible (nonobstant les particularités individuelles) s'étend globalement entre 16 Hz et 16000 Hz. Ça fait quand même un sacré paquet de notes potentielles. Imaginez vous diriger une chorale de moines grégoriens et annoncer « bien, nous allons nous chanter un petit Dies iræ à 5282 Hz ».
Que dire des orchestres ? À partir du moment où vous regroupez des voix, des instruments à corde, à vent, etc. si vous voulez obtenir une quelconque harmonie, il faut bien se mettre d'accord sur un sous-ensemble limité de fréquences « autorisées » sur lesquelles tout le monde devra se caler. Et puis, il faut bien trouver un moyen pour synchroniser tout ce beau monde.
Au fil des siècles, le système musical a donc évolué, et c'est pourquoi, lorsque vous ouvrez un bouquin sur le sujet, vous trouverez les concepts de notes, gammes, de modes, d'accords, d'armures à la clé, etc. Tâchons de débroussailler tout ça.
Les notes
Le premier outil que propose la théorie musicale est la note. Il existe une infinité de fréquences audibles, mais on facilite grandement les choses si on n'en garde que quelques unes et qu'on leur donne des noms. Ainsi, si un compositeur me demande de jouer un « Do », je sais que je dois émettre un son correspondant à la fréquence du « Do », peu importe que ce soit avec un ukulélé, un biniou ou une flute à bec. D'ailleurs, je n'ai même plus besoin d'avoir conscience de la notion de fréquence : j'ai simplement besoin de savoir où placer mes doigts pour « jouer un Do ».
Bien ! Sur l'infinité de fréquences audibles, quel sous-ensemble sélectionner ? Si je ne sélectionne pas assez de notes, je ne pourrai pas jouer de mélodies subtiles ; si j'en sélectionne trop, je perds le bénéfice de la simplification et je complexifie grandement la fabrication d'instruments. Par ailleurs, il serait bon que les notes à ma disposition me permettent de jouer des intervalles consonants tels que nous les avons étudiés plus haut. Enfin, faut-il entre chaque note un écart constant ? La question peut paraître bête, parce que nous n'avons jamais connu d'autre système : si vous tapez sur chaque touche du clavier d'un piano dans l'ordre, la même hauteur sépare chaque paire de notes successives ; mais ça n'est pas la seule façon de sélectionner des notes et historiquement, c'est même un fait assez récent.
Historiquement, toutes les méthodes de sélection de notes ont utilisé la même façon de procéder : le découpage de l'octave.
On a dit que deux sons séparés d'une octave étaient tellement consonants qu'on pouvait considérer qu'il représentent en fait la même note. Ainsi, pour découper mon spectre audible en notes, il me suffit de suivre les étapes suivantes.
D'abord, je sélectionne une fréquence de manière tout à fait arbitraire, au hasard 440 Hz. Je ne garde que les fréquences entre cette note et l'octave supérieure (donc entre 440 et 880 Hz). Je sélectionne un certain nombres de fréquences à l'intérieur de l'octave (peu importe comment), auxquelles je donne de jolis petits noms (Do, Re, Mi…). Et c'est tout.
Ensuite, si j'ai besoin de notes plus aiguës, il me suffit de reproduire le même découpage à l'octave supérieure (880 ~ 1760 Hz), et supérieure, et supérieure, etc. Idem, si j'ai besoin de notes plus basses, je divise les fréquences par deux pour obtenir l'octave inférieure, et inférieure, etc.
Pour distinguer les différents Do, les Si, les Mi entre eux, on les numérote. Ainsi, le La3 correspond à une fréquence de 440 Hz, La4 de 880 Hz, La5 de 1760 Hz, La2 de 220 Hz, etc.
Aujourd'hui, la fréquence de référence est effectivement La3 à 440 Hz, et c'est un standard iso. D'où l'expression « donnez-moi le la ». À d'autres époques, d'autres fréquences étaient utilisées. Vous serez peut-être aussi surpris que moi d'apprendre que certaines personnes pensent réellement que si le La3 vaut 440 Hz et pas 432 Hz, c'est à cause d'un complot nazi…
Le découpage de l'octave
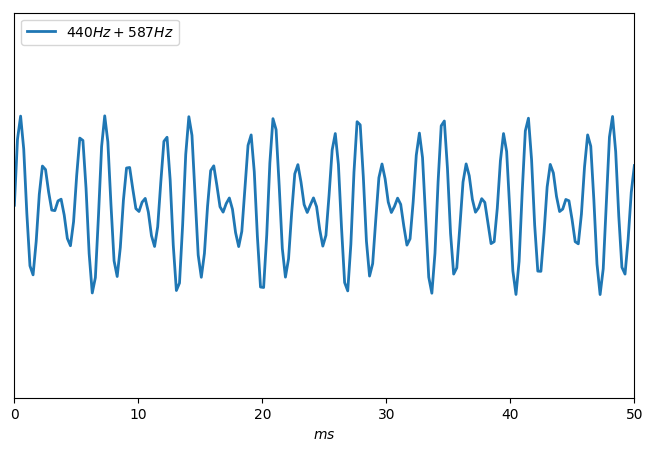
Au sein d'une seule octave [440;880[ quelles fréquences retenir pour en faire des notes ? Notre système actuel s'est arrêté sur les suivantes :

| Fréquence | Nom |
|---|---|
| 440 Hz | La |
| 466.16 Hz | La♯ ou Si♭ |
| 493.88 Hz | Si |
| 523.25 Hz | Do |
| 554.36 Hz | Do♯ ou Ré♭ |
| 587.33 Hz | Ré |
| 622.25 Hz | Ré♯ ou Mi♭ |
| 659.26 Hz | Mi |
| 698.46 Hz | Fa |
| 739.99 Hz | Fa♯ ou Sol♭ |
| 783.99 Hz | Sol |
| 830.61 Hz | Sol♯ ou La♭ |
| 880 Hz | La |
Vous noterez que j'ai inclus la dernière ligne uniquement pour montrer qu'on retombe bien sur l'octave ; nous avons bel et bien 12 notes disponibles au sein de notre octave.
La composition du clavier du piano reflète cette sélection.
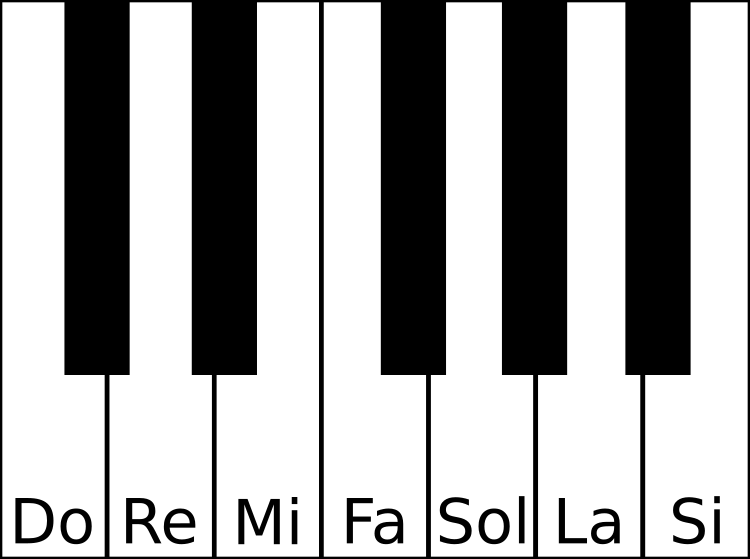
De ce tableau, plusieurs observations intéressantes.
D'abord, seules sept notes possèdent des noms propres « Do », « Ré »… les autres sont indiquées au moyen des « altérations » dièse (♯) et bémol (♭). « Fa♯ » signifie « la note à mi-chemin entre Fa et la note suivante, i.e Sol ». « Mi♭ » signifie « la note à mi-chemin entre Mi et la note précédente, i.e Ré ». Pourquoi seules sept notes portent-elles des noms ? Pourquoi dispose-t-on de deux altérations alors qu'à priori une seule suffirait ? Nous allons y revenir. Les noms en eux-mêmes sont arbitraires, d'ailleurs les anglo-saxons utilisent les lettres « A », « B », etc. On ne s'en préoccupera pas.
Ensuite, vous remarquerez qu'il s'agit d'une suite géométrique et non arithmétique. Entre les deux premières notes, on a un écart de 26.15 Hz, entre les deux dernières, 49.39 Hz. C'est parce qu'on a choisi d'avoir un « écart de perception constant » entre les notes et on l'a dit plus haut, la relation entre fréquence et hauteur perçue n'est pas linéaire mais logarithmique. Si je veux douze notes au sein de mon octave, et que l'écart entre chaque note soit perçu comme équivalent, il faut que le rapport entre deux fréquences successives soit égal à 12√2 ≈ 1.059. Parce que 440 * 12√2 * 12√2 * … (12 fois) … * 12√2 = 880.
Enfin, vous remarquerez qu'il n'y a pas toujours le même écart entre deux notes nommées. Ainsi, il y a une note intermédiaire entre Do et Ré ou entre Ré et Mi, mais pas entre Mi et Fa ou Si et Do. Cela se concrétise par l'absence de touche noire entre ces notes sur le clavier du piano. Pourquoi avoir créé des notes avec des écarts différents ? Là encore, « c'est historique ».
Mais bordel, pourquoi douze notes ?!? Pourquoi seules sept d'entre elles portent des noms ? Pourquoi des écarts différents entre les notes ?
Pourquoi douze notes ? Pourquoi sept notes ?
Il faut que vous sachiez que j'ai travaillé des mois sur ce billet, parcouru la moitié des forums de la planète pour trouver une réponse satisfaisante énoncée clairement à cette question, et je n'ai pas réussi. Et vous, vous vous pointez la bouche en cœur en espérant que la réponse va vous tomber tout cru dans le bec ? Sachez que j'ai grande envie de vous secouer comme un prunier en criant « C'est compliquuuuéééééééééééé !!! ». Je vais expliquer la chose telle que je l'ai comprise.
Donc, pourquoi avons nous 7 notes (do, ré, mi, fa, sol, la, si) et pourquoi divisons nous l'octave en 12 ?
Et bien c'est à cause des grecs (c'est toujours de la faute des grecs) et plus particulièrement de Pythagore (c'est toujours de la faute à Pythagore). Pythagore est communément reconnu par les vulgarisateurs comme le premier péquenaud à avoir tenté de découper l'octave pour construire une sélection de notes. Voici comment il s'y est pris.
Partons d'une fréquence, n'importe laquelle, par exemple 100 Hz. Notez que Pythagore ne résonnait pas en terme de fréquence mais de longueur de corde, mais ça revient au même. Prenons maintenant la fréquence séparée d'une quinte (100 Hz * 3/2 = 150 Hz) car rappelons que la quinte est l'intervalle le plus consonant après l'octave. De cette nouvelle fréquence, nous augmentons encore d'une quinte (150 * 3/2 = 225) mais comme cela nous emmène en dehors de l'octave de départ [100 Hz;200 Hz[, nous divisons le résultat par deux. Et nous procédons ainsi de suite encore et encore. Et, par un hasard mathématique miraculeux, au bout de douze fois, nous retombons presque sur la note de départ puisque nous obtenons 101.36 Hz (tout le bazar qui va suivre déroule de ce « presque »).
Ces douze fréquences sont réparties de manière suffisamment uniformes pour pouvoir servir de système de base pour accorder un instrument, et forment la gamme Pythagoricienne.
Ladite gamme présente quelques inconvénients : d'abord, l'intervalle qui s'approche le plus de la tierce n'est pas une « vraie » tierce et s'en éloigne au point que la dissonance devient audible. Ensuite, les notes sont irrégulièrement réparties, ce qui fait que pour transposer une mélodie (la décaler vers les graves ou les aigus), il faut réaccorder tout l'instrument.
Pour en savoir plus sur la construction de la fameuse gamme pythagoricienne, je vous redirige vers quelques ressources pertinentes.
https://www.easyzic.com/dossiers/la-gamme-de-pythagore,h151.html https://www.youtube.com/watch?v=cTYvCpLRwao
Avec les âges, d'autres théoriciens de la musique ont tenté de modifier le découpage de l'octave pour contourner les problèmes de la gamme de Pythagore, mais le nombre douze est resté, à la fois de par son implantation historique, mais aussi car un tel découpage offre des propriétés mathématiques et harmoniques intéressantes que nous allons voir plus loin.
Quant aux sept notes, j'ai trouvé plusieurs explications. Je préfère celle du Tétracorde. Il est dit que les mêmes grecs antiques utilisaient une espèce de harpe à quatre cordes. Les deux cordes extérieures étaient toujours espacées d'un intervalle de quarte, mais les deux cordes intérieures pouvaient être accordées de diverses manières en fonction de l'émotion que l'on souhaitait provoquer, toujours en respectant les intervalles harmoniques proposés par Pythagore.
En « collant » deux harpes identiquement accordées à une quinte d'écart, on obtenait ainsi un total de huit notes possibles réparties inégalement sur une octave complète.
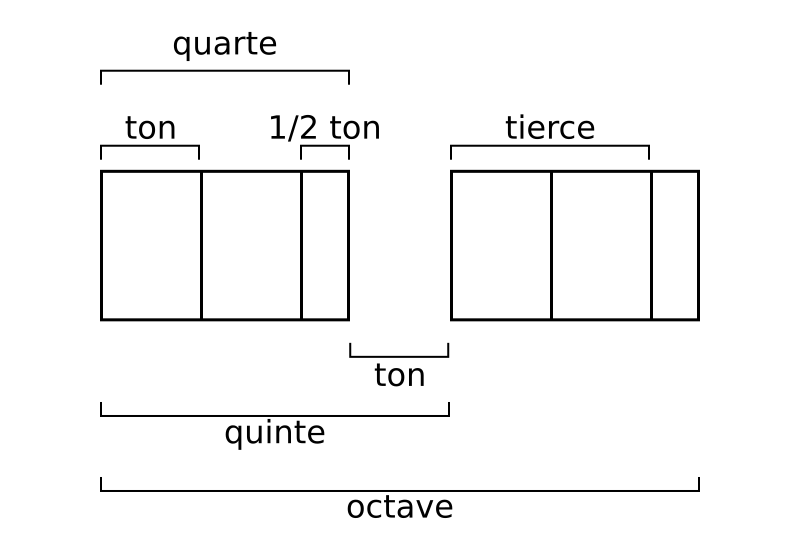
Cette manière de ne conserver que sept notes et de les répartir ainsi possède tellement de propriétés intéressantes qu'elle a survécu de la Grèce antique jusqu'à nos jours. En n'utilisant que sept notes, tous les intervalles consonants sont présents : la tierce, la quarte, la quinte, l'octave, etc. Quant au ton, c'est la différence entre la quinte et la quarte. Le demi-ton égal la moitié d'un ton :) Et tous les intervalles peuvent être produit en additionnant des tons et demi-tons.
Notez également que nos huit notes sont séparées par un certain nombre de tons et de demi-tons, et qu'il existe un grand nombre de possibilités pour répartir ces demi-tons au sein de l'octave. Sur le schéma, nous avons TTDTTTD (T = ton, D = demi-ton), mais nous aurions pu effectuer une autre sélection, par exemple TDTTDTT. Ces différentes répartitions permettaient de donner des « teintes » différentes aux mélodies, étaient appelés « modes » et portaient chacune un nom spécifique (Dorien, Lydien, Mixolydien, Lapincrétin, etc.)
La théorie moderne a conservé grosso-modo deux modes : le mode ionien (honnêtement, le nom, on s'en fout complètement) correspond à la répartition illustrée sur le schéma (TTDTTTD), est aujourd'hui appelé « mode majeur » et a servi de base lorsqu'on a décidé de donner des noms aux notes.
Ensuite, le mode éolien (TDTTDTT) qu'on appelle aujourd'hui « mode mineur » (les plus sagaces d'entre vous auront remarqué qu'il s'agit de la même répartition, mais décalée, c'est à dire qu'on démarre au « La » au lieu du « Do ». C'est ce mode qu'ont utilisé les anglo-saxons pour nommer leurs notes (A, B, C…) et c'est pourquoi le « La » correspond à la lettre « A ».
Ces éléments culturels, avec un fort ancrage dans les règles objectives de l'harmonie, ont perduré jusqu'à aujourd'hui : quand on écrit de la musique, on utilise sept notes, réparties irrégulièrement sur l'octave, mais on découpe néanmoins ladite octave en douze et les cinq notes intercalaires ont un rôle moins « fonctionnel » et plus « décoratif ». Le résultat le plus évident est que le système de notation musical est complètement absurde et rend l'étude de la musique bien plus complexe que nécessaire.
Le tempérament égal
Maintenant équipés de ce bagage culturel, nous pouvons revenir au système actuel avec une oreille neuve. Intéressons nous au tempérament égal.
Quizz ! Qu'est-ce que le tempérament égal ?
- A. Le petit surnom que lui donne sa copine au Dalaï Lama.
- B. Le syndrome dépressif chez les profs. de maths en collège.
- C. Un lama génétiquement modifié pour ne jamais cracher.
- D. Le système actuellement en vigueur pour découper l'octave.
Pendant un long moment dans l'histoire, les instruments étaient accordés pour jouer des intervalles justes. D'un point de vue harmonique, c'était le pied intégral, mais ça posait aussi pas mal de problèmes pratiques puisque ça signifiait qu'il n'y avait pas exactement le même écart entre chaque paire de notes. Par conséquent, dès que vous souhaitiez transposer une mélodie (la décaler vers les graves ou les aigus) et bien vous étiez obligé de réaccorder l'instrument.
Au bout d'un certain nombre de siècles, avec la démocratisation des instruments de musique, la simplicité et la praticité l'ont emporté sur la pureté harmonique : on a décidé d'accorder les instruments avec des intervalles égaux entre toutes les notes, quitte à ce que certains intervalles soient un poil moins consonants qu'ils devraient l'être.
Et c'est la raison pour laquelle, aujourd'hui, il y a toujours la même hauteur (à l'oreille) entre deux touches adjacentes d'un piano. C'est ce qu'on appelle le « tempérament égal ».
Voici un tableau qui reprend, pour chacune des douze notes, le rapport de sa fréquence par rapport à la première.
| Note | Distance en demi-tons | Rapport | Nom de l'intervalle | Rapport « simple » le plus proche |
|---|---|---|---|---|
| Do | 0 | 1.000 | Unisson | 1 (1/1) |
| Do♯ ou Ré♭ | 1 | 1.059 | Demi-ton ou Seconde mineure | 1.066 (16/15) |
| Ré | 2 | 1.122 | Ton ou Seconde majeure | 1.125 (9/8) |
| Ré♯ ou Mi♭ | 3 | 1.189 | Tierce mineure | 1.200 (6/5) |
| Mi | 4 | 1.260 | Tierce majeure | 1.250 (5/4) |
| Fa | 5 | 1.335 | Quarte juste | 1.333 (4/3) |
| Fa♯ ou Sol♭ | 6 | 1.414 | Quarte augmentée ou Quinte diminuée | 1.400 (7/5) |
| Sol | 7 | 1.498 | Quinte juste | 1.500 (3/2) |
| Sol♯ ou La♭ | 8 | 1.587 | Sixte mineure | 1.6 (8/5) |
| La | 9 | 1.682 | Sixte majeure | 1.667 (5/3) |
| La♯ ou Si♭ | 10 | 1.782 | Septième mineure | 1.778 (16/9) |
| Si | 11 | 1.888 | Septième majeure | 1.875 (15/8) |
| Do | 12 | 2.000 | Octave juste | 2 (2/1) |
Vous noterez que, par un pur hasard mathématique, certaines des notes sélectionnées tombent presque sur des rapports entiers simples consonants. Ainsi, entre deux notes séparées par cinq demi-tons, on a presque une quarte parfaite, par sept demi-tons presque une quinte. Notez qu'entre quatre demi-tons, on a une tierce, mais l'écart avec la « vraie » tierce est un peu plus important.
Ce que cela signifie, c'est que sur un piano actuel, il est tout simplement impossible de jouer une tierce parfaitement consonante. Ainsi, supposons un genre musical comme le Barbershop Quartet ou les différentes voix sont espacées d'intervalles harmoniquement justes, un piano sera incapable de s'aligner parfaitement. Soit le piano et le chanteur ne jouent pas exactement la même note, soit le chanteur s'aligne sur celle du piano. Dans tous les cas, on peut dire qu'il y a un organe génital mâle dans le potage. Seule notre culture musicale et la grande adaptabilité du cerveau nous a appris à tolérer ce type d'écart.
L'avantage de ce système, en revanche, est qu'il devient bien plus facile de fabriquer et d'accorder des instruments de musique. Il est également très facile de transposer de la musique, c'est à dire décaler une mélodie un peu plus haut ou un peu plus bas, opération impossible (ou nécessitant un réaccordage complet de l'instrument) dans un système ou les intervalles entre les notes ne sont pas constants.
Le tempérament égal, qui ne s'est généralisé que très récemment dans l'histoire, n'est pas harmoniquement juste, et est une affaire de compromis.
Notez également comme ça devient le bazar pour nommer les intervalles. Les livres de musique nous disent que « Un intervalle tire son nom du nombre de degrés qu'il contient… ». Do - Ré - Mi = une tierce. Ré - Mi - Fa = une tierce aussi. Mais pas la même tierce puisqu'en pratique, le nombre de demi-tons est différent. On doit donc accoler un qualificatif au nom de l'intervalle (Majeur, Mineur, Augmenté, Diminué, etc.) pour préciser le nombre de demi-tons.
Que ce système n'ait pas été simplifié depuis ne cesse de me laisser pantois.
Partitions, clés, armures à la clé
Sans l'éclairage des éléments historiques présentés plus haut, certains éléments du solfège sont pour le moins déconcertants. Ainsi le concept d'armure à la clé m'a longtemps plongé dans une confusion similaire à celle d'un élu LREM se questionnant sur l'intérêt du droit des salariés.
Je ne vais pas expliquer le concept de portée, d'autres font ça très bien.
Vous noterez toutefois qu'il est complètement farfelu d'utiliser une échelle linéaire pour indiquer des éléments non linéaires.
En effet, les lignes de la portée permettent d'accueillir les notes dans l'ordre (do, ré, mi, etc.). Mais, on l'a vu, lesdites notes ne sont en fait pas toutes espacées de la même façon. Certaines notes sont séparées par des tons, d'autres par des demi-tons.
Que se passe-t-il si je souhaite transposer une mélodie, c'est à dire la décaler vers les aigus ou vers les graves ? Car ce qui fait une mélodie, c'est l'écart des notes entre elles, par leurs hauteurs exactes. Au clair de la Lune chanté par Barry White ou Maria Callas, c'est toujours Au clair de la Lune.
Un esprit naïf et ignorant penserait qu'il suffit de décaler les notes vers le haut ou vers le bas sur la portée. Mais alors, la mélodie ne serait plus vraiment la même car les intervalles d'une note à l'autre ne seraient plus respectés.

Sur ma première portée, une simple mélodie composée de trois notes : « sol -ton- la -ton- si ». Si je décale toutes les notes d'un cran vers le haut, j'obtiens « la -ton- si -demi-ton- do », une mélodie différente. Ma transposition est fausse.
Pour corriger le tir, puisqu'on change la note de départ, il faut également changer la répartition des tons et demi-tons entre les notes.
La gamme « par défaut », on l'a vu plus haut, est la gamme de do majeur. C'est à dire qu'on a la répartition suivante : do -ton- ré -ton- mi -demi-ton- fa -ton- sol -ton- la -ton- si -demi-ton- do…
Notre mélodie démarrait sur « sol », on l'a transposée pour démarrer sur « la », soit un ton d'écart.
Pour déterminer le nouveau jeu de notes disponibles, au lieu de partir de do, on va donc partir de ré, et en conservant la répartition des tons et demi-tons, on obtient les sept notes suivantes :
ré -ton- mi -ton- fa♯ -demi-ton- sol -ton- la -ton- si -ton- do♯ -demi-ton- ré…
Ainsi, pour transposer une mélodie écrite « en do » d'un ton vers le haut, il faut passer « en ré » ce qui revient à dire que tous les fa et tous les do doivent être joués un demi-ton plus haut.
Il serait fastidieux d'écrire, sur la portée, un dièse à côté de chaque do et chaque fa. On a donc le concept d'« armure à la clé » : on indique les notes censées être diésées une bonne fois pour toute.
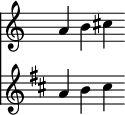
Cette sélection de notes utilisables est appelée une « gamme ». En « gamme de do majeur », j'utilise do, ré, mi, fa, sol, la, si. En « gamme de ré majeur », j'utilise do♯, ré, mi, fa♯, sol, la, si. L'important est que dans les deux cas, la répartition des tons et des demi-tons dans la gamme est identique.
Le nombre de dièses (ou de bémols) présents permettent de savoir dans quelle gamme est composé le morceau. On parle d'« armure à la clé ».
Les accords
Un autre outil très important proposé par la musique moderne est la notion d'accord. On a dit qu'en jouant plusieurs sons consonants, on obtenait un seul son plus riche que la somme des parties. Donc, plutôt que de jouer des notes individuelles, on va jouer des empilements de notes qu'on appelle « accords ».
On ne parle d'accords qu'à partir de trois notes.
Grâce au travail que nous avons réalisé plus haut, nous comprenons les raisons de la consonance, et nous savons que si nous voulons jouer plusieurs notes consonantes, il nous suffit de les espacer d'intervalles consonants.
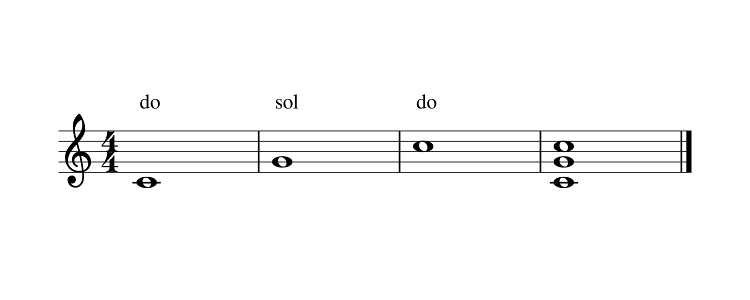
Par exemple, je peux jouer une note, e.g « Do », sa quinte, i.e « Sol » et son octave i.e le « Do » du dessus. La consonance est parfaite.
Tellement parfaite, à vrai dire, que ça sonne un peu « plat ». Par ailleurs, comme on considère que deux « Do » sont une seule note, ça ne compte pas vraiment, il faut se contenter des notes présentes à l'intérieur de l'octave.
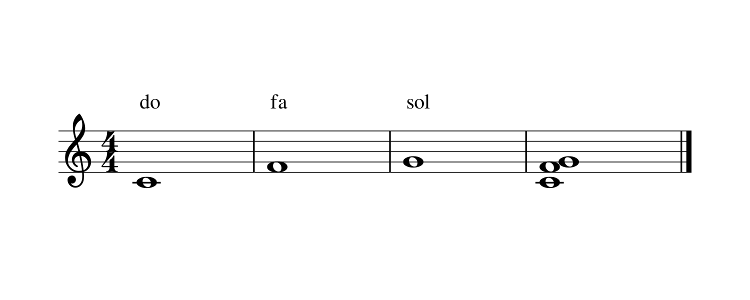
Je pourrais jouer la note (do), sa quarte (fa) et sa quinte (sol), car la quarte est également très consonante. Oui, mais entre fa et sol, il y a un ton, et cet intervalle n'est pas particulièrement consonant.
Pour accorder trois notes consonantes deux à deux, le système actuel s'est arrêté sur l'accord tierce + quinte. Pour un accord de do, je joue do, sa tierce i.e mi, sa quinte i.e sol. Ainsi, entre do et mi, il y a quatre demi-tons, donc une tierce majeure ; entre mi et sol, il y en a trois, soit une tierce mineure.
Un tel type d'accord est appelé « accord parfait majeur ». C'est à peu près ce qu'on peut obtenir de plus consonant dans le tempérament égal. C'est également l'accord correspondant aux toutes premières harmoniques de n'importe quel son, il y a donc une forte justification concrète à cette construction.
Une légère variation de cet accord s'appelle l'accord parfait mineur, et se fait en jouant une note, sa tierce mineure et sa quinte juste, par exemple Do, Mi♭ et Sol, ce qui revient à inverser la tierce majeure et la tierce mineure. La tierce mineure étant un intervalle moins consonant, l'accord parfait mineur est moins consonant que l'accord parfait majeur, et est fréquemment utilisé dans un contexte musical ou l'on souhaite apporter une atmosphère plus triste, dramatique, ou tout simplement plus chargée en émotion.
On utilise traditionnellement la notation anglo-saxonne pour indiquer les accords. Ainsi, l'accord parfait majeur de Do se note « C », et l'accord parfait mineur de Do se note « Cm ».
La note qui donne naissance à l'accord (la « première note ») est appelée la fondamentale.
Partant de cette base, il existe de nombreuses variations qui consistent à rajouter des tierces (accords de plus de trois notes) et/ou utiliser des intervalles différents entre les notes, ce qui permet de constituer tout un « bestiaire d'accords » (augmentés, diminués, suspendus, de septième, etc.), chaque type possédant une sonorité et une notation propre. La description et l'étude de ces constructions n'apporteraient pas grand chose à notre propos, aussi nous nous en passerons.

Pause récapitulative
Le moment est venu de faire une nouvelle pause récapitulative. Tous les éléments que nous venons de voir (tempérament, notes, gammes, modes, accords, etc.) sont les outils de base proposés par la théorie musicale moderne occidentale afin de rationaliser et faciliter la création de musique. Basés sur les lois naturelles de l'harmonie, ils permettent aux musicien·nes et à leur audience de s'affranchir des concepts ardus de suite harmonique et de rapport entre les fréquences pour réfléchir à un niveau d'abstraction plus élevé.
Pour m'accompagner sur la « Bamba Triste » au Ukulélé, il me suffit de savoir que je dois jouer un accord G à tel moment et un accord D7 à tel autre. C'est quand même plus facile que de calculer à quelles fréquences en Hz doivent vibrer mes cordes.
Ces briques de base sont utilisées de manières diverses et variées en fonction des genres musicaux, lesquels peuvent parfois être définis par des règles additionnelles spécifiques.
Mais disposer d'un tas de briques et quelques sacs de ciment ne signifie pas nécessairement que l'on sache construire une maison. De même, empiler les accords au hasard ne suffira peut-être pas à écrire un tube qui vous rendra riche et célèbre sur Youtube.
Pour aller plus loin, nous allons nous intéresser à l'une des branches de la musique que l'on nomme « musique tonale ».
Musique tonale, fonctions musicales
Nous nous sommes intéressé·es au « quoi » et au « comment » mais pas au « pourquoi ». Jusqu'à maintenant, nous n'avons pas fait de distinction entre un « Do », un « Mi » ou un « Sol », entre un accord de Ré ou un accord se Fa.
Mais la musique est une construction, un enchaînement de notes et d'accords destiné à raconter une histoire et provoquer une réponse émotive. La musique tonale est la branche de la musique moderne qui s'interroge sur le sens que peuvent posséder les notes et leurs relations entre elles. À partir de cette réflexion, il est possible d'assigner aux notes et accords, au sein d'une gamme donnée, des fonctions utilitaires qui seront utilisées dans des contextes spécifiques.
J'avoue que j'ai eu du mal à comprendre le schmilblick au départ, et cette comparaison m'a beaucoup aidé :
Raconter une bonne histoire nécessite de suivre certaines règles. Ainsi, on part en général d'une situation initiale, puis survient un élément perturbateur qui va déclencher certaines péripéties et la résolution permettra le retour à une situation finale satisfaisante. Ce type de séquence est en général imbriqué sur plusieurs niveaux dans les romans, il y a des péripéties dans les péripéties. C'est cet enchaînement de situations stables et de tensions qui nous tient en haleine et rend le roman ou le film intéressants.
Une bonne musique est un peu comme une bonne histoire et repose en grande partie sur la même alternance. Ainsi, en jouant un accord initial, par exemple un accord de Do, je vais « poser une situation initiale » à laquelle l'oreille s'habitue. Ensuite, une succession d'accords plus ou moins dissonants va créer une tension de plus en plus importante et finalement, on revient à l'accord de départ ce qui confère une impression d'achèvement et de retour à la normale. Écoutez cet exemple très simple qui pourrait correspondre à la fin de n'importe quelle chanson populaire.

Ainsi, au sein de la gamme de Do majeur, l'accord de Do n'est pas juste l'accord de Do, c'est « l'accord qui va permettre de poser la situation initiale » et l'accord de Sol est « l'accord qui vient foutre le boxon et créer de la tension ».
J'espère que l'idée est assez claire. Voyons un peu comment cela fonctionne, et quelles sont les raisons harmoniques qui justifient cette construction.
Gammes et degrés
Notez que je vais commencer par présenter le vocabulaire technique avant d'aborder le sens que tout ceci peut avoir.
Le concept de musique tonale repose sur les gammes heptatoniques (composée de sept notes) diatoniques (composée de notes séparées de tons et de demi-tons) que nous avons étudié plus haut. C'est à dire les modes majeurs et mineurs.
Dans une gamme, les notes sont placées dans l'ordre. Le numéro de la note dans la gamme s'appelle son degré et on le note traditionnellement à l'aide de chiffres romains. À chaque degré correspond un rôle et chaque rôle dispose de son petit nom.
Voici l'exemple avec la gamme de Do majeur.

| Note | Degré | Rôle |
|---|---|---|
| Do | I | Tonique |
| Ré | II | Sus-tonique |
| Mi | III | Médiante |
| Fa | IV | Sous-dominante |
| Sol | V | Dominante |
| La | VI | Sus-dominante |
| Si | VII | Sensible |
Les rôles les plus importants sont ceux de la tonique et de la dominante et dans une légère moindre mesure, la sous-dominante et la sensible.
Tonique et Dominante, deux pôles complémentaires
On l'a vu, cette gamme est telle qu'elle est parce que chacune de ses notes présente un intervalle remarquable à peu près consonant par rapport à la tonique.
En écoutant de la musique, mon cerveau, inconsciemment, va chercher à déterminer la tonalité de l'œuvre, c'est à dire le point central par rapport auquel une harmonie existe.
Dans une musique écrite en tonalité de Do, toutes les notes et accords qui ne sont pas « do » provoquent une impression d'instabilité et de tension, tandis que le retour à la tonique provoque l'impression de stabilité, d'achèvement, d'accomplissement, de repos, d'arrivée. Ainsi, beaucoup de chansons / musiques modernes démarrent et terminent par la tonique, qui constitue le degré le plus important de la gamme, et par rapport auquel les autres rôles sont définis.
L'autre note la plus importante est la dominante : celle-ci est séparée de la tonique par une quinte, et présente donc une très forte consonance, tout en en étant très éloignée : en effet, si j'égrène les notes de la gamme « do, ré, mi, fa » je m'éloigne de la tonique, mais dès que je dépasse la dominante « sol, la, si, do… », je m'en approche à nouveau (même si à l'octave au dessus).
En résumé, la tonique est la note qui pose le contexte, qui sert de point de référence, tandis que la dominante est celle qui offre le plus de tension.
Voici une autre métaphore pour illustrer ces deux rôles : si une chanson était une randonnée, la tonique serait le point de départ, tandis que la dominante correspondrait au refuge de montagne : c'est le point culminant de la balade, c'est là qu'on va prendre les plus belles photos et c'est aussi un endroit ou l'on peut s'arrêter et poser les sacs, mais il faudra bien redescendre un jour ou l'autre.
Je ne suis pas certain que ce soit bien clair aussi étudions un exemple : vous connaissez probablement la chanson « Frère Jacques ».

Essayez d'observer à quels endroits les notes Do (la tonique) et Sol (la dominante) sont utilisées dans la chanson.
On démarre par « Frè-re Jac-cques » (bis), chaque syllabe « Frè » et « cques » correspond à un Do. Immédiatement, le contexte est posé, nous sommes dans la tonalité de Do, et la tension musicale reste relativement basse.
On enchaîne avec « Dor-mez voooouuuus ? » (bis) et chaque « vous » correspond à un Sol. On sent bien que ce « vous » est le moment ou la tension mélodique est à son comble. Peut-être que le pauvre camarade de chambrée du frère Jacques vient de se rendre compte que son réveil n'a pas sonné et que toute la promo risque de se faire priver de dessert par le père supérieur. Son incrédulité et sa panique sont palpables, d'autant que demain, c'est tarte aux framboises.
On poursuit avec « Son-nez les ma-ti-nes » (bis), une phrase qui démarre par un Sol et redescend vers le Do de départ. L'accent mis sur la première syllabe est cohérent avec l'emploi de la dominante, et confère à la requête une atmosphère urgente. Néanmoins, on sent que la tension redescend et qu'on se redirige vers une situation stable : « Maintenant, Frère Jacques, arrêtez de déconner et sonnez ces cloches qu'on puisse aller prier un bon coup avant de retourner se coucher ! ».
On termine avec « Ding Dang Dong » Do - Sol - Do. Finir sur la Tonique permet de retrouver un état stable. Essayez d'imaginer une autre note, et vous constateriez que ça ne serait pas aussi satisfaisant.
L'analyse est certes un peu tirée par les cheveux mais montre bien qu'on peut voir tonique et dominante comme deux pôles ayant chacun des rôles opposés et complémentaires dans la chanson. Ces notes ne sont pas placées là au hasard, elles sont utilisées parce qu'elles ont un sens d'un point de vue mélodique et harmonique.
Sous-dominante et sensible, deux rôles support
Attaquons nous maintenant aux deux autres degrés principaux : la sous-dominante et la sensible.
La sous-dominante est appelée ainsi car elle est… sous la dominante, bravo à ceux qui suivent. La sous-dominante est surtout séparée de la tonique par une quarte, l'intervalle le plus stable après la quinte. Il y a donc autant d'écart entre la tonique et la dominante qu'entre la sous-dominante et la tonique de l'octave supérieure.
On pourrait dire que la sous-dominante a le même rôle que la dominante, mais qu'elle le remplit un peu moins efficacement : la tension qu'elle évoque n'est pas aussi importante, sa stabilité n'est pas aussi avérée… Dans la métaphore de la randonnée, la dominante pourrait représenter le refuge du sommet tandis que la sous-dominante n'est que le refuge de mi-parcours. Pas la fin du parcours, mais une étape sympa.
Enfin, il reste la sensible. Ce degré porte ce nom car c'est la note la plus proche de la tonique : elle n'en est séparée que par un demi-ton. Or, le fonctionnement de notre audition fait que, lorsque l'on entend une note aussi proche de la tonique, le cerveau rouspète et « réclame » la tonique. C'est un peu comme si on vous servait un bon plat de spaghettis carbonara en ayant oublié les lardons.
Le retour de la sensible à la tonique provoque donc une importante sensation de résolution, une propriété qui sera fort utile comme nous le verrons plus loin.
Harmonisation de la gamme
Dans la musique, on peut distinguer la mélodie de l'harmonie.
La mélodie, c'est l'enchaînement de notes individuelles qui forment l'« air » de la chanson, celui que vous pouvez siffloter ou qui vous reste dans la tête (Dans la basse-cour il-y-a…).
L'harmonie, c'est la toile de fond sonore qui sert à « décorer », si on peut dire.
Exemple : dans la chanson « Over the rainbow », la mélodie est constituée des notes chantées par Iz (soooom… wheeeeere… o… ver… the… rain… bow…), l'harmonie est constituée des toing woing tou twing wing joués au Ukulélé.
On pourrait dire que la mélodie est le sujet du tableau, tandis que l'harmonie constitue le décor.
Bien ! Nous avons étudié le rôle des degrés de la gamme dans le cadre mélodique, mais les choses deviennent encore plus intéressantes quand on s'intéresse au côté harmonique.
Puisque nous n'allons plus jouer des notes individuelles mais des accords, nous allons, pour chaque degré de la gamme, construire un accord tout bête en empilant deux tierces, comme nous l'avons vu plus haut.
Chaque accord est noté en fonction de son degré, et on utilise les majuscules pour les accords majeurs, les minuscules pour les accords mineurs.

Les plus sagaces d'entre vous auront remarqué que certains de ces accords sont des accords parfaits majeurs, d'autres sont des accords parfaits mineurs, en fonction de la répartition des tons et demi-tons dans la gamme. Notez l'exception du dernier accord, qui n'est ni majeur ni mineur mais diminué, car il est constitué d'une tierce mineure et d'une quinte diminuée (si si, comptez les demi-tons). C'est un peu le vilain petit canard et son rôle est particulier.
Gamme de Do majeur :
| Note | Degré | Rôle | Accord | Notation de l'accord |
|---|---|---|---|---|
| Do | I | Tonique | C | I |
| Ré | II | Sus-tonique | Dm | ii |
| Mi | III | Médiante | Em | iii |
| Fa | IV | Sous-dominante | F | IV |
| Sol | V | Dominante | G | V |
| La | VI | Sus-dominante | Am | vi |
| Si | VII | Sensible | Bdim | vii° |
Les plus sagaces parmi les sagaces noteront que puisque les positions des tons et demi-tons sont constantes dans la gamme, alors à chaque degré correspond toujours le même type d'accord, quelque soit l'accord exact associé. Par exemple avec la gamme de Ré majeur, notez que la dernière colonne est identique à celle du tableau précédent.
Gamme de Ré majeur :
| Note | Degré | Rôle | Accord | Notation de l'accord |
|---|---|---|---|---|
| Ré | I | Tonique | D | I |
| Mi | II | Sus-tonique | Em | ii |
| Fa♯ | III | Médiante | F♯m | iii |
| Sol | IV | Sous-dominante | G | IV |
| La | V | Dominante | A | V |
| Si | VI | Sus-dominante | Bm | vi |
| Do♯ | VII | Sensible | C♯dim | vii° |
Ces éléments nous permettent de raisonner en terme de progression d'accords : de nombreuses chansons populaires modernes sont simplement constituées d'accords, joués les uns après les autres dans des progressions plus ou moins complexes et plus ou moins originales.
Et comme ce qui nous intéresse, c'est la relation d'un accord à l'autre, on utilise les numéros d'accords plutôt que leurs valeurs concrètes. Ainsi, la progression I -> IV -> V vaudra C -> F -> G en gamme de do, A -> D -> E en gamme de la, D -> G -> A en gamme de ré, etc.
Le groupe Axis of Awesome est fréquemment cité en illustration pour ce medley de chansons populaires utilisant toutes la progression I-V-vi-IV.
Vous je ne sais pas, mais je trouve que ça permet de rendre l'apprentissage d'un instrument beaucoup moins intimidant, parce qu'un nombre incalculable de chansons sont jouables en ne maîtrisant que deux, trois ou quatre accords.
Progression d'accords
La notion de progression d'accords n'est guère complexe à comprendre : vous jouez un accord, puis un autre, puis un autre, et chaque progression possède sa sonorité propre. Pour écrire une chanson, vous pouvez tâcher de créer votre propre progression, ou piocher dans l'immense bibliothèque de progressions plus ou moins populaires que vous trouverez un peu partout sur le Web.
Certaines progressions sont tellement classiques qu'elles disposent de leurs noms propres, comme l'Anatole ou le blues à 12 mesures.
Mais il nous reste à étudier pourquoi le saut d'un accord à l'autre fonctionne (ou pas). Et pour cela, il nous faut regarder ce qui se passe note à note d'un accord à l'autre.
I et V
Le changement d'accord le plus important est celui qui consiste à passer de l'accord I à l'accord V, et vice-versa.
En gamme de Do, cela nous donne les progressions d'accord : C -> G et G -> C.
Pourquoi le passage de l'un à l'autre est il aussi intéressant ?
Rappelons que :
- l'accord de do (C) est constitué des notes do-mi-sol ;
- l'accord de sol (G) est constitué des notes sol-si-ré.
D'abord, rappelons que les fondamentales de ces accords (do et sol) constituent la tonique et la dominante de la gamme et que fatalement, les accords basés sur ces notes partagent leurs caractéristiques.
Ainsi, passer de I à V créé une tension qui reste harmoniquement plaisante mais néanmoins immanquable. Par ailleurs, la fondamentale de C (do) n'est pas présente dans G, ce qui accentue cette impression d'éloignement.
En revanche, la fondamentale de G (sol) est bien présente dans C, ce qui créé un point d'ancrage et génère une certaine stabilité entre les deux.
Enfin, l'accord V contient la note sensible de la gamme (ici, si). On l'a vu, la sensible résout sur la tonique, cela contribue à conférer au mouvement V -> I une très forte impression de résolution, de « retour à la maison ».

I et IV
Analysons les liens entre accords de tonique et accord de sous-dominante.
En gamme de Do :
- l'accord C est constitué de do-mi-sol ;
- l'accord F est constitué de fa-la-do;
Notons que la note do est présente dans les deux accords, ce qui confère une certaine stabilité au passage de l'un à l'autre.
De la même manière qu'il n'y a qu'un demi-ton entre la sensible et la tonique, il y a le même demi-ton entre mi et fa. Cela contribue à faciliter le changement I -> IV.
Le mouvement IV -> I provoque une certaine impression de résolution, mais pas autant que le mouvement V -> I, car l'accord IV ne contient ni la sensible, ni la dominante.
D'un point de vue fonctionnel, l'accord de sous-dominante est souvent utilisé comme un point de passage, un accord préparatoire qui sert d'étape intermédiaire entre I et V.

V7, I et IV
L'accord V est souvent utilisé dans sa forme septième, ce qui revient à dire qu'il s'agit d'un accord de quatre notes au lieu de trois.
Ainsi, en gamme de Do, l'accord G7 est constitué des notes sol-si-ré-fa.
Entre si et fa, il y a trois tons (on parle de triton) et l'on considère que cet intervalle présente une forte dissonance, ce qui confère à l'accord de septième un fort caractère, et accentue l'effet de tension de l'accord.
L'utilisation de la forme septième présente plusieurs avantages.
G7 contient à la fois la dominante et la sous-dominante (sol et fa) de la gamme, aussi le passage de F à G7 est facilité.
Pour la même raison, l'impression de résolution du mouvement G7 -> I est encore amplifiée.
V7, c'est un peu la version super-sayen de V…

vii° et V7
Le rôle de l'accord vii° est un peu particulier.
En gamme de Do :
- vii° = Bdim -> si-ré-fa.
- V7 = G7 -> sol-si-ré-fa.
vii° est constitué d'un triton (empilement de deux tierces mineures) et est considéré comme assez dissonant. Par ailleurs, si l'on regarde bien, Bdim est équivalent à G7 auquel il manquerait la fondamentale.
Pour ces raisons, on considère généralement que l'accord vii° n'a pas de fonction harmonique particulière et est en fait une version « cassée » de V7. Il est de fait assez peu utilisé.
Substitutions d'accords
Nous avons évoqués les accords I, IV, V et dans une moindre mesure, vii°. Et les autres ? Les pauvres ii, iii, vi, sont-ils donc condamnés à ne servir à rien ? Que nenni ! Car il existe un mécanisme nommé la substitution d'accords et qui nous permet d'une manière plus ou moins cavalière de substituer un accord par un autre.
On considère généralement que deux accords dont les fondamentales sont séparés de deux notes sont fonctionnellement substituables.
Prenons l'exemple de l'accord I en do majeur, donc C.
C est constitué des notes do-mi-sol. La fondamentale est Do. Deux notes au dessus, c'est Mi. Deux notes au dessous, c'est La.
L'accord de Mi (Em) est constitué des notes mi-sol-si.
L'accord de La (Am) est constitué des notes la-do-mi.
Vous noterez que Em et Am partagent deux notes en commun avec C. C et Em partagent mi et sol. C et Am partagent do et mi.
| Do | Ré | Mi | Fa | Sol | La | Si | |
|---|---|---|---|---|---|---|---|
| Am | * | * | * | ||||
| C | * | * | * | ||||
| Em | * | * | * |
Le fait d'avoir les deux tiers des notes en commun font que ces accords possèdent une sonorité relativement proche, et l'on considère généralement que leurs fonctions sont similaires.
Ainsi, on considère que les accords iii et vi peuvent avoir une fonction tonique et parfois se substituer à I.
Pour les mêmes raisons, on constate que IV partage deux notes avec ii et vi. Toutefois, on considère que seul ii peut endosser le rôle de sous-dominante, parce que vi a déjà un rôle de tonique.
Idem, iii et vii° partagent deux notes avec V, mais iii a déjà un rôle de tonique, et on a déjà vu que vii° n'est finalement qu'un V7 amputé.
Ainsi, il est possible de procéder à quelques substitutions pour apporter un peu de variété et de diversité à sa progression d'accords.
À l'aune de ces explications, je vous laisse le soin d'analyser cette progression d'accords ultra-courante déjà mentionnée.

Dominante secondaire
Il existe un autre concept fréquemment utilisé dans les progressions d'accords, c'est celui de dominante secondaire.
Voici un exemple.
C
Ce soir j'attends Madeleine
G7
J'ai apporté du lilas
G7
J'en apporte toutes les semaines
C
Madeleine elle aime bien ça
C
Ce soir j'attends Madeleine
G7
On prendra le tram trente-trois
G7
Pour manger des frites chez Eugène
C
Madeleine elle aime tant ça
C7
Madeleine c'est mon Noël
F
C'est mon Amérique à moi
D7
Même qu'elle est trop bien pour moi
G7
Comme dit son cousin Joël
C
Ce soir j'attends Madeleine
…
Analysons la progression d'accords de cette sublime chanson du non moins sublime Brel.
Au cours des premières phrases, on alterne régulièrement entre les accords C et G7 et vous aurez probablement reconnu les accords I et V7 de la gamme de Do majeur. Rien de nouveau ici.
Les choses deviennent intéressantes quand on arrive sur « Madeleine, elle aime tant ça ». Nous sommes sur l'accord de tonique quand soudain, Brel enchaîne avec « Madeleine, c'est mon Noël… » sur un accord C7. Ouate de Phoque ! Que vient foutre ici cet accord C7 ? Il ne fait pas partie de notre gamme ?!
Pour comprendre ce qui se passe, il faut étudier la suite. On enchaîne avec « C'est mon Amérique à moi » sur un accord F. F, c'est l'accord IV de la gamme de Do majeur, mais il y a quelque chose d'intéressant dans le mouvement C7 -> F. Devinerez-vous quoi ? Comptez le nombre de degrés entre F et C.
Il y en a cinq ! Ce qui signifie que C7 est l'accord de dominante de la gamme de Fa majeur. Autrement dit, C7 est à F ce que G7 est à C.
Ainsi, la progression C -> G7 -> C -> C7 -> F, que l'on serait tenté d'analyser comme I -> V7 -> I -> I7 -> IV doit en fait être prise comme I -> V7 -> I -> V/IV -> V. La notation V/IV signifie « l'accord de dominante de l'accord IV ».
Si l'on continue l'analyse, on trouve un autre exemple juste après. Entre « même qu'elle est trop bien pour moi » et « Comme dit son cousin Joël », on a la progression d'accord D7 -> G7. Vous aurez compris que D7 est la dominante de la dominante. La progression D7 -> G7 s'analyse comme V/V -> V.
Ce mécanisme qui consiste à intercaler une dominante secondaire pour retomber sur un accord de la gamme est extrêmement courant et présente un double avantage. D'abord, cela augmente l'impression de résolution au passage d'un accord à l'autre. Ensuite, cela permet de créer des modulations, c'est à dire passer d'une gamme à l'autre sans que ça se voie trop.
Ainsi, quand j'utilise la progression d'accord C -> C7 -> F, la résolution entre C7 et F est tellement forte que l'oreille pourrait presque oublier que la tonalité de la chanson est C, ce qui me permettrait d'utiliser à loisir et pour un temps les accords de la gamme de Fa.
Ainsi, loin de fermer ses frontières, la musique tonale s'enrichit en accueillant à bras ouverts les accords étrangers (prends en de la graine, Gérard Collomb).

Conclusion
J'ai envie de m'arrêter là, d'abord parce que je bosse sur ce billet depuis des mois et que j'en ai marre ; ensuite parce que plus je trouve de la matière à rajouter, plus je tombe sur de nouvelles questions sans réponses ; enfin parce que j'ai l'impression que les éléments expliqués ici permettent de répondre aux objectifs du billet : même si je n'ai finalement fait qu'effleurer les racines d'un art millénaire, cela devrait permettre à chacun·e de poursuivre ses propres recherches avec des bases solides.
Pour terminer, j'ai envie de dire que la musique, c'est simple et complexe en même temps.
Cela m'a beaucoup aidé de ne plus voir la théorie musicale moderne comme un ensemble de règles et recettes immuables à apprendre par cœur et appliquer bêtement mais de plutôt la considérer comme un ensemble d'outils plus ou moins élaborés permettant au plus grand nombre de composer et d'apprécier rapidement de la musique.
Partant de là, libre à chacun de se faire sa propre culture et de chercher à aller plus loin.
Edit Merci à Pascal Borreli pour la relecture orthographique.